题目内容
 已知二次函数h(x)=ax2+bx+c(c>0),其导函数y=h′(x)的图象如图所示,f(x)=lnx-h(x).
已知二次函数h(x)=ax2+bx+c(c>0),其导函数y=h′(x)的图象如图所示,f(x)=lnx-h(x).(1)求函数f(x)在x=1处的切线斜率;
(2)若函数f(x)在区间(
| 1 |
| 2 |
| 1 |
| 4 |
(3)若函数y=2x-ln x(x∈[1,4])的图象总在函数y=f(x)的图象的上方,求c的取值范围.
分析:(1)由导函数y=h′(x)的图象过点A,B,可求出h′(x),从而可求出f′(x),f′(1),即所求斜率;
(2)利用导数求出f(x)的单调区间,则区间(
,m+
)为其一单调区间的子集,由此可解;
(3)函数y=2x-ln x(x∈[1,4])的图象总在函数y=f(x)的图象的上方,等价于2x-ln x>f(x)在x∈[1,4]上恒成立,分离参数后转化为函数最值问题处理即可.
(2)利用导数求出f(x)的单调区间,则区间(
| 1 |
| 2 |
| 1 |
| 4 |
(3)函数y=2x-ln x(x∈[1,4])的图象总在函数y=f(x)的图象的上方,等价于2x-ln x>f(x)在x∈[1,4]上恒成立,分离参数后转化为函数最值问题处理即可.
解答:解:(1)由题知,h′(x)=2ax+b,其图象为直线,
且过A(2,-1)、B(0,3)两点,
∴
,解得
.
∴h(x)=-x2+3x+c.∴f(x)=ln x-(-x2+3x+c)=x2-3x-c+ln x.
∴f′(x)=2x-3+
,∴f′(1)=2-3+
=0,
所以函数f(x)在x=1处的切线斜率为0.
(2)由题意可知,函数f(x)的定义域为(0,+∞),
由(1)知,f′(x)=2x-3+
=
=
.
令f′(x)=0,得x=
或x=1.
当x变化时,f(x)、f′(x)随x的变化情况如下表:
∴f(x)的单调递增区间为(0,
),(1,+∞);f(x)的单调递减区间为(
,1).
要使函数f(x)在区间(
,m+
)上是单调函数,
则
,解得
<m≤
.
故实数m的取值范围是(
,
].
(3)由题意可知,2x-lnx>x2-3x-c+lnx在x∈[1,4]上恒成立,
即当x∈[1,4]时,c>x2-5x+2lnx恒成立.
设g(x)=x2-5x+2lnx,x∈[1,4],则c>g(x)max.易知g′(x)=2x-5+
.令g′(x)=0得,x=
或x=2.
当x∈(1,2)时,g′(x)<0,函数g(x)单调递减;当x∈(2,4)时,g′(x)>0,函数g(x)单调递增.
而g(1)=12-5×1+2ln 1=-4,g(4)=42-5×4+2ln 4=-4+4ln 2,
显然g(1)<g(4),故函数g(x)在[1,4]上的最大值为g(4)=-4+4ln 2,故c>-4+4ln 2.
∴c的取值范围为(-4+4ln 2,+∞).
且过A(2,-1)、B(0,3)两点,
∴
|
|
∴h(x)=-x2+3x+c.∴f(x)=ln x-(-x2+3x+c)=x2-3x-c+ln x.
∴f′(x)=2x-3+
| 1 |
| x |
| 1 |
| 1 |
所以函数f(x)在x=1处的切线斜率为0.
(2)由题意可知,函数f(x)的定义域为(0,+∞),
由(1)知,f′(x)=2x-3+
| 1 |
| x |
| 2x2-3x+1 |
| x |
| (2x-1)(x-1) |
| x |
令f′(x)=0,得x=
| 1 |
| 2 |
当x变化时,f(x)、f′(x)随x的变化情况如下表:
| x | (0,
|
|
(
|
1 | (1,+∞) | ||||||
| f′(x) | + | 0 | - | 0 | + | ||||||
| f(x) | ?↗ | 极大值 | ?↘ | 极小值 | ?↗ |
| 1 |
| 2 |
| 1 |
| 2 |
要使函数f(x)在区间(
| 1 |
| 2 |
| 1 |
| 4 |
则
|
| 1 |
| 4 |
| 3 |
| 4 |
故实数m的取值范围是(
| 1 |
| 4 |
| 3 |
| 4 |
(3)由题意可知,2x-lnx>x2-3x-c+lnx在x∈[1,4]上恒成立,
即当x∈[1,4]时,c>x2-5x+2lnx恒成立.
设g(x)=x2-5x+2lnx,x∈[1,4],则c>g(x)max.易知g′(x)=2x-5+
| 2 |
| x |
| 1 |
| 2 |
当x∈(1,2)时,g′(x)<0,函数g(x)单调递减;当x∈(2,4)时,g′(x)>0,函数g(x)单调递增.
而g(1)=12-5×1+2ln 1=-4,g(4)=42-5×4+2ln 4=-4+4ln 2,
显然g(1)<g(4),故函数g(x)在[1,4]上的最大值为g(4)=-4+4ln 2,故c>-4+4ln 2.
∴c的取值范围为(-4+4ln 2,+∞).
点评:本题考查了导数的几何意义及导数与函数单调性的关系,注意不等式恒成立的等价表述方式,解决不等式恒成立常转化为函数最值问题解决.

练习册系列答案
相关题目
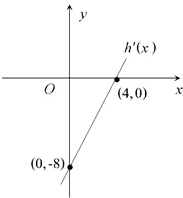 已知二次函数h(x)=ax2+bx+c(其中c<3),其导函数y=h′(x)的图象如图,f(x)=6lnx+h(x).
已知二次函数h(x)=ax2+bx+c(其中c<3),其导函数y=h′(x)的图象如图,f(x)=6lnx+h(x). (2014•达州一模)已知二次函数h(x)=ax2+bx+c(其中c<3),其导函数y=h′(x)的图象如图,f(x)=6lnx+h(x).
(2014•达州一模)已知二次函数h(x)=ax2+bx+c(其中c<3),其导函数y=h′(x)的图象如图,f(x)=6lnx+h(x).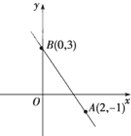 (第三、四层次学校的学生做次题)
(第三、四层次学校的学生做次题)