题目内容
已知A为三角形的内角,且满足sinA+cosA=| 1 | 5 |
(Ⅰ)求sinA、cosA、tanA的值; (Ⅱ)求sin3A-cos3A的值.
分析:(Ⅰ)由A为三角形的内角,且满足sinA+cosA=
,可得1+2sinAcosA=
,又 cos2A+sin2A=1,
解得cosA,sinA,tanA的值.
(Ⅱ)由立方差 sin3A-cos3A=(sinA-cosA) (sin2A+sinAcosA+cos2A),把cosA,sinA 的值代入运算.
| 1 |
| 5 |
| 1 |
| 25 |
解得cosA,sinA,tanA的值.
(Ⅱ)由立方差 sin3A-cos3A=(sinA-cosA) (sin2A+sinAcosA+cos2A),把cosA,sinA 的值代入运算.
解答:解:(Ⅰ)∵A为三角形的内角,且满足sinA+cosA=
,∴1+2sinAcosA=
,
又 cos2A+sin2A=1,∴cosA=-
,sinA=
,tanA=-
.
(Ⅱ) sin3A-cos3A=(sinA-cosA) (sin2A+sinAcosA+cos2A)=
(1-
)=
.
| 1 |
| 5 |
| 1 |
| 25 |
又 cos2A+sin2A=1,∴cosA=-
| 3 |
| 5 |
| 4 |
| 5 |
| 4 |
| 3 |
(Ⅱ) sin3A-cos3A=(sinA-cosA) (sin2A+sinAcosA+cos2A)=
| 7 |
| 5 |
| 12 |
| 25 |
| 91 |
| 125 |
点评:本题考查同角三角函数的基本关系,立方差公式的应用,求出sinA 和cosA 的值,是解题的关键.

练习册系列答案
相关题目
 的( )
的( )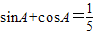 .
.