题目内容
已知A为三角形的内角,则sinA>
是cosA<
的( )
| 1 |
| 2 |
| ||
| 2 |
分析:先由sinA>
,cosA<
,分别求出A的范围是:
<A<
,
<A<π,
再再根据“谁大谁必要,谁小谁充分”的原则,即可确定答案.
| 1 |
| 2 |
| ||
| 2 |
| π |
| 6 |
| 5π |
| 6 |
| π |
| 6 |
再再根据“谁大谁必要,谁小谁充分”的原则,即可确定答案.
解答:解:由于A为三角形的内角,则0<A<π,
∵sinA>
,∴
<A<
,
∵cosA<
,∴
<A<π
由于{A|
<A<
}
{A|
<A<π},
则sinA>
是cosA<
的充分不必要条件.
故答案为A.
∵sinA>
| 1 |
| 2 |
| π |
| 6 |
| 5π |
| 6 |
∵cosA<
| ||
| 2 |
| π |
| 6 |
由于{A|
| π |
| 6 |
| 5π |
| 6 |
| ? |
| ≠ |
| π |
| 6 |
则sinA>
| 1 |
| 2 |
| ||
| 2 |
故答案为A.
点评:本题考查的是必要、充分及充要条件的判定.由判断充要条件的方法,我们可知命题“x∈A”是命题“x∈B”的充分不必要条件,则A
B.
| ? |
| ≠ |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 的( )
的( )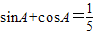 .
.