题目内容
给出下列命题
(1)实数的共轭复数一定是实数;
(2)满足|z-i|+|z+i|=2的复数z的轨迹是椭圆;
(3)若m∈Z,i2=-1,则im+im+1+im+2+im+3=0;
其中正确命题的序号是( )
(1)实数的共轭复数一定是实数;
(2)满足|z-i|+|z+i|=2的复数z的轨迹是椭圆;
(3)若m∈Z,i2=-1,则im+im+1+im+2+im+3=0;
其中正确命题的序号是( )
分析:(1)利用共轭复数的定义,可以判断;(2)利用|Z+i|+|Z-i|=2的几何意义,得到Z的轨迹是线段;(3)利用m∈Z,i2=-1,化简可求.
解答:解:(1)根据共轭复数的定义,实数的虚部为0,故(1)正确;利用|z-i|+|z+i|=2表示复数Z对应的点Z到点A(0,-1)和到点B(0,1)的之和等于2=|AB|,得到Z的轨迹是线段,故(2)错;im+im+1+im+2+im+3=im+im+1-im-im+1=0,故(3)正确.故选C.
点评:本题考查共轭复数的定义、两个复数差的绝对值的几何意义,复数
与复平面内对应点之间的关系,复数的模的定义,判断条件代表的几何意义,是解题的关键
与复平面内对应点之间的关系,复数的模的定义,判断条件代表的几何意义,是解题的关键

练习册系列答案
相关题目
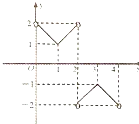 已知函数y=f(x)(x∈R且x≠2n,n∈Z)是周期为4的函数,其部分图象如图,给出下列命题:
已知函数y=f(x)(x∈R且x≠2n,n∈Z)是周期为4的函数,其部分图象如图,给出下列命题: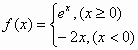 ,则关于x的方程f[f(x)]+k=0,给出下列命题:
,则关于x的方程f[f(x)]+k=0,给出下列命题: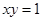 ,则
,则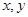 互为倒数”的逆命题;(2)“面积相等的三角形全等”的否命题;
互为倒数”的逆命题;(2)“面积相等的三角形全等”的否命题; 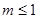 ,则
,则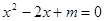 有实根”的逆否命题;
有实根”的逆否命题;
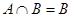 ,则
,则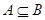 ”的逆否命题.
”的逆否命题.