题目内容
例3.设f(x)=x2-x+m,log2f(a)=2,f(log2a)=m,a>0且a≠1解不等式组
|
分析:利用已知条件列出关于a,m的方程组,正确求解出m的值,将不等式组转化为关于x的不等式组,进而确定出不等式组的解集.
解答:解:由已知条件,可以得到f(a)=4,且(log2a)2-(log2a)+m=m,
根据后者,解出log2a=0或1,得出a=1(舍)或a=2,
将a=2代入f(a)=4得到22-2+m=4?m=2.因此,f(x)=x2-x+2.
从而所求解的不等式组可化为
?
,
进一步得到不等式组的解集为(0,1).
故所求不等式的解集为(0,1).
根据后者,解出log2a=0或1,得出a=1(舍)或a=2,
将a=2代入f(a)=4得到22-2+m=4?m=2.因此,f(x)=x2-x+2.
从而所求解的不等式组可化为
|
|
进一步得到不等式组的解集为(0,1).
故所求不等式的解集为(0,1).
点评:本题考查了学生解方程组的基本功,考查了等价转化的思想,解决过程中注意对数式有意义的隐含条件,最后利用数轴确定出不等式组的解集.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
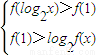 .
.