题目内容
满足条件AB=6,AC=2BC的三角形ABC的面积的最大值为
12
12
.分析:建立坐标系,求出C的轨迹方程,即可求得三角形面积的最大值.
解答: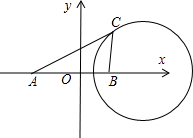 解:建立如图所示的坐标系,则A(-3,0),B(3,0)
解:建立如图所示的坐标系,则A(-3,0),B(3,0)
设C(x,y),则
∵AC=2BC,∴
=2
化简可得(x-5)2+y2=16
即C的轨迹是一(5,0)为圆心,4为半径的圆,
∴三角形ABC的面积的最大值为
×6×4=12
故答案为:12
 解:建立如图所示的坐标系,则A(-3,0),B(3,0)
解:建立如图所示的坐标系,则A(-3,0),B(3,0)设C(x,y),则
∵AC=2BC,∴
| ||
|
化简可得(x-5)2+y2=16
即C的轨迹是一(5,0)为圆心,4为半径的圆,
∴三角形ABC的面积的最大值为
| 1 |
| 2 |
故答案为:12
点评:本题考查三角形面积的计算,考查轨迹方程,属于中档题.

练习册系列答案
相关题目
四棱锥P-ABCD中,AD⊥面PAB,BC⊥面PAB,底面ABCD为梯形,AD=4,BC=8,AB=6,∠APD=∠CPB,满足上述条件的四棱锥的顶点P的轨迹是( )
| A、圆的一部分 | B、椭圆的一部分 | C、球的一部分 | D、抛物线的一部分 |
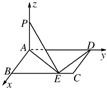 9、已知矩形ABCD中AB=3,BC=a,若PA⊥平面AC,在BC边上取点E,使PE⊥DE,则满足条件的E点有两个时,a的取值范围是
9、已知矩形ABCD中AB=3,BC=a,若PA⊥平面AC,在BC边上取点E,使PE⊥DE,则满足条件的E点有两个时,a的取值范围是
 已知椭圆C:
已知椭圆C: