题目内容
(1)已知:tanα=- ,求
,求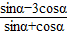 的值;
的值;(2)已知α∈(0,
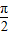 ),
),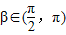 sin
sin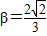 ,sin(α+β)=
,sin(α+β)= ,求cosα的值.
,求cosα的值.
【答案】分析:(1)所求式子分子分母除以cosα,利用同角三角函数间的基本关系化为关于tanα的关系式,将tanα的值但仍旧是即可求出值;
(2)由β的范围及sinβ的值,利用同角三角函数间的基本关系求出cosβ的值,再由α与β的范围,及sin(α+β)的值,利用同角三角函数间的基本关系求出cos(α+β)的值,所求式子cosα变形为cos[(α+β)-β],利用两角和与差的余弦函数公式化简,把各自的值代入计算即可求出值.
解答:解:(1)∵tanα=- ,
,
∴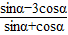 =
=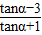 =
=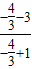 =13;
=13;
(2)∵β∈(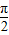 ,π),sinβ=
,π),sinβ=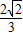 ,
,
∴cosβ=-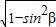 =-
=- ,
,
∵α∈(0,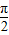 ),β∈(
),β∈(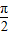 ,π),
,π),
∴α+β∈( ,
,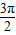 ),
),
∵sin(α+β)= ,
,
∴cos(α+β)=- =-
=- ,
,
∴cosα=cos[(α+β)-β]=cos(α+β)cosβ+sin(α+β)sinβ=-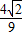 ×(-
×(- )+
)+ ×
×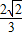 =
=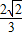 .
.
点评:此题考查了两角和与差的余弦函数公式,以及同角三角函数间的基本关系,熟练掌握公式及基本关系是解本题的关键.
(2)由β的范围及sinβ的值,利用同角三角函数间的基本关系求出cosβ的值,再由α与β的范围,及sin(α+β)的值,利用同角三角函数间的基本关系求出cos(α+β)的值,所求式子cosα变形为cos[(α+β)-β],利用两角和与差的余弦函数公式化简,把各自的值代入计算即可求出值.
解答:解:(1)∵tanα=-
 ,
,∴
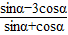 =
=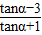 =
=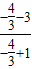 =13;
=13;(2)∵β∈(
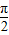 ,π),sinβ=
,π),sinβ=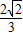 ,
,∴cosβ=-
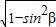 =-
=- ,
,∵α∈(0,
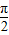 ),β∈(
),β∈(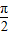 ,π),
,π),∴α+β∈(
 ,
,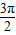 ),
),∵sin(α+β)=
 ,
,∴cos(α+β)=-
 =-
=- ,
,∴cosα=cos[(α+β)-β]=cos(α+β)cosβ+sin(α+β)sinβ=-
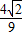 ×(-
×(- )+
)+ ×
×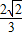 =
=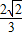 .
.点评:此题考查了两角和与差的余弦函数公式,以及同角三角函数间的基本关系,熟练掌握公式及基本关系是解本题的关键.

练习册系列答案
相关题目