题目内容
已知函数f(x)=
,给出下列三个命题:
①函数f(x)为偶函数;
②存在xi∈R(i=1,2,3),使得以点(xi,f(xi))(i=1,2,3,4)为原点的三角形是等腰直角三角形;
③存在xi∈R(i=1,2,3),使得以点(xi,f(xi))(i=1,2,3,4)为原点的四边形为菱形.
其中所有真命题的个数是( )
|
①函数f(x)为偶函数;
②存在xi∈R(i=1,2,3),使得以点(xi,f(xi))(i=1,2,3,4)为原点的三角形是等腰直角三角形;
③存在xi∈R(i=1,2,3),使得以点(xi,f(xi))(i=1,2,3,4)为原点的四边形为菱形.
其中所有真命题的个数是( )
| A、无内容 | B、1 | C、2 | D、3 |
分析:①由偶函数的定义进行判断.
②由解析式做出大致图象:根据图象和等腰直角三角形的性质,进行判断即可;
③取两个自变量是有理数,使得另外两个无理数差与两个有理数的差相等,即可得出此四边形为平行四边形.
②由解析式做出大致图象:根据图象和等腰直角三角形的性质,进行判断即可;
③取两个自变量是有理数,使得另外两个无理数差与两个有理数的差相等,即可得出此四边形为平行四边形.
解答:解:①若x为有理数,则-x也为有理数,∴f(x)=f(-x)=1,
若x为无理数,则-x也为无理数,∴f(x)=f(-x)=0,
综上有f(x)=f(-x),∴函数f(x)为偶函数,∴①正确.
②根据f(x)=
,可知:
假设存在等腰直角三角形ABC,则斜边AB只能在x轴上或在直线y=1上,且斜边上的高始终是1,
不妨假设A,B在x轴上,如图
故斜边AB=2,故点A、B的坐标不可能是无理数,否则O点不再是中点,故不存在.
另外,当AB在y=1上,C在x轴时,由于AB=2,则C的坐标应是有理数,
故假设不成立,即不存在符合题意的等腰直角三角形,②错误;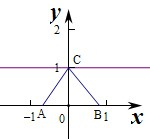
③根据②做出的图形知,
取两个自变量是有理数,使得另外两个无理数差与两个有理数的差相等,
即可画出平行四边形,且是对角线相互垂直,
可以做出以点(xi,f(xi))(i=1,2,3,4)为顶点的四边形为菱形,③正确.
故选:C.
若x为无理数,则-x也为无理数,∴f(x)=f(-x)=0,
综上有f(x)=f(-x),∴函数f(x)为偶函数,∴①正确.
②根据f(x)=
|
假设存在等腰直角三角形ABC,则斜边AB只能在x轴上或在直线y=1上,且斜边上的高始终是1,
不妨假设A,B在x轴上,如图
故斜边AB=2,故点A、B的坐标不可能是无理数,否则O点不再是中点,故不存在.
另外,当AB在y=1上,C在x轴时,由于AB=2,则C的坐标应是有理数,
故假设不成立,即不存在符合题意的等腰直角三角形,②错误;

③根据②做出的图形知,
取两个自变量是有理数,使得另外两个无理数差与两个有理数的差相等,
即可画出平行四边形,且是对角线相互垂直,
可以做出以点(xi,f(xi))(i=1,2,3,4)为顶点的四边形为菱形,③正确.
故选:C.
点评:本题主要考查分段函数的应用,考查学生的 推理和想象能力,综合性较强,难度较大.

练习册系列答案
相关题目
已知函数f(x)=
,g(x)=1+
,若f(x)>g(x),则实数x的取值范围是( )
| 1 |
| |x| |
| x+|x| |
| 2 |
| A、(-∞,-1)∪(0,1) | ||||
B、(-∞,-1)∪(0,
| ||||
C、(-1,0)∪(
| ||||
D、(-1,0)∪(0,
|