题目内容
(2011•南京模拟)设b,c表示两条直线,α,β表示两个平面,现给出下列命题:
①若b?α,c∥α,则b∥c;
②若b?α,b∥c,则c∥α;
③若c∥α,α⊥β,则c⊥β;
④若c∥α,c⊥β,则α⊥β.
其中正确的命题是
①若b?α,c∥α,则b∥c;
②若b?α,b∥c,则c∥α;
③若c∥α,α⊥β,则c⊥β;
④若c∥α,c⊥β,则α⊥β.
其中正确的命题是
④
④
.(写出所有正确命题的序号)分析:由题设条件,对四个选项逐一判断即可,①选项用线线平行的条件进行判断;②选项用线面平行的条件判断;③选项用线面垂直的条件进行判断;④选项用面面垂直的条件进行判断,
解答:解:①选项不正确,因为线面平行,面中的线与此线的关系是平行或者异面;
②选项不正确,因为与面中一线平行的直线与此面的关系可能是在面内或者与面平行;
③选项不正确,因为两面垂直,与其中一面平行的直线与另一面的关系可能是平行,在面内也可能垂直;
④选项正确,因为线与面平行,线垂直于另一面,可证得两面垂直.
其中正确的命题是④.
故答案为:④.
②选项不正确,因为与面中一线平行的直线与此面的关系可能是在面内或者与面平行;
③选项不正确,因为两面垂直,与其中一面平行的直线与另一面的关系可能是平行,在面内也可能垂直;
④选项正确,因为线与面平行,线垂直于另一面,可证得两面垂直.
其中正确的命题是④.
故答案为:④.
点评:本题考查空间中直线与平面之间的位置关系,求解本题关键是有较好的空间想像能力,对空间中点线面的位置关系可以准确判断,再就是熟练掌握点线面位置关系判断的定理与条件.

练习册系列答案
相关题目
 (2011•南京模拟)阅读下列算法语句:输出的结果是
(2011•南京模拟)阅读下列算法语句:输出的结果是 (2011•南京模拟)A.选修4-1几何证明选讲
(2011•南京模拟)A.选修4-1几何证明选讲 和
和 均不能成立
均不能成立 和
和 和(a+
和(a+ )2>(b+
)2>(b+ )2均不能成立
)2均不能成立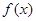 =
=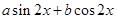 ,其中a,b
,其中a,b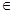 R,ab
R,ab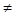 0,若
0,若 对一切则x
对一切则x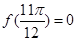 ;②
;②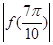 <
<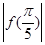 ;③
;③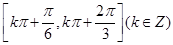 ;⑤存
;⑤存