题目内容
已知直线y=(a+1)x-1与曲线y2=ax恰有一个公共点,求实数a的值.
答案:
解析:
提示:
解析:
|
解:由方程组 (a+1)2x2-(3a+2)x+1=0. (1)当a=-1时,x=-1, ∴ (2)当a≠-1时,由Δ=(3a+2)2-4(a+1)2=0, 得a=0或a= 综上,当a=0或a=-1或a= |
提示:
|
首先考虑两方程联立成方程组,在求解过程中通过对a的讨论来研究两曲线公共点的情况. |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
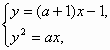 得
得 (m>n>0)相交于A,B两点,若弦AB的中点的横坐标等于
(m>n>0)相交于A,B两点,若弦AB的中点的横坐标等于 ,则双曲线
,则双曲线 的两条渐近线的夹角的正切值等于_______.
的两条渐近线的夹角的正切值等于_______.