题目内容
(本小题满分13分)设函数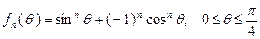 ,其中
,其中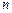 为正整数.
为正整数.
(Ⅰ)判断函数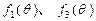 的单调性,并就
的单调性,并就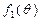 的情形证明你的结论;
的情形证明你的结论;
(Ⅱ)证明: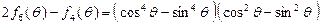 ;
;
(Ⅲ)对于任意给定的正整数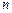 ,求函数
,求函数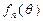 的最大值和最小值.
的最大值和最小值.
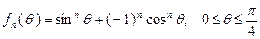 ,其中
,其中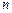 为正整数.
为正整数.(Ⅰ)判断函数
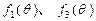 的单调性,并就
的单调性,并就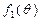 的情形证明你的结论;
的情形证明你的结论;(Ⅱ)证明:
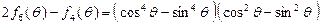 ;
;(Ⅲ)对于任意给定的正整数
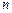 ,求函数
,求函数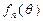 的最大值和最小值.
的最大值和最小值.(Ⅰ)函数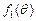 在
在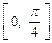 上单调递增(Ⅱ)略 (Ⅲ)
上单调递增(Ⅱ)略 (Ⅲ)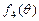 的最大值为
的最大值为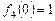 ,最小值为
,最小值为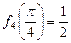 .
.
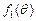 在
在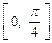 上单调递增(Ⅱ)略 (Ⅲ)
上单调递增(Ⅱ)略 (Ⅲ)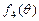 的最大值为
的最大值为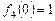 ,最小值为
,最小值为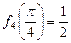 .
.:(1)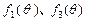 在
在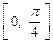 上均为单调递增的函数. 1分
上均为单调递增的函数. 1分
对于函数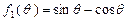 ,设
,设 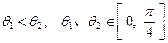 ,则
,则
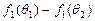
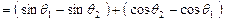 ,
,
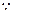
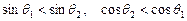 ,
,
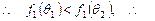 函数
函数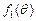 在
在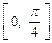 上单调递增. 3分
上单调递增. 3分
(2) 原式左边
原式左边 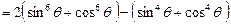
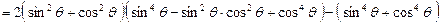
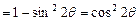 .… 5分
.… 5分
又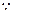 原式右边
原式右边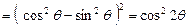 .
.
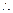
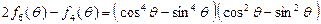 . 6分
. 6分
(3)当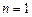 时,函数
时,函数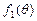 在
在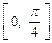 上单调递增,
上单调递增,
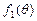 的最大值为
的最大值为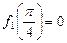 ,最小值为
,最小值为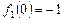 .
.
当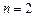 时,
时,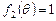 ,
, 函数
函数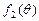 的最大、最小值均为1.
的最大、最小值均为1.
当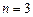 时,函数
时,函数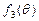 在
在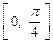 上为单调递增.
上为单调递增.
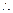
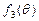 的最大值为
的最大值为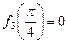 ,最小值为
,最小值为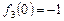 .
.
当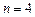 时,函数
时,函数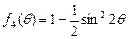 在
在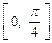 上单调递减,
上单调递减,
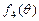 的最大值为
的最大值为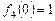 ,最小值为
,最小值为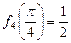 . … 9分
. … 9分
下面讨论正整数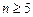 的情形:
的情形:
当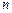 为奇数时,对任意
为奇数时,对任意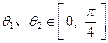 且
且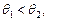
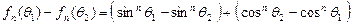 ,
,
以及 ,
,
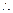
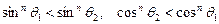 ,从而
,从而 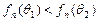 .
.
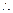
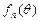 在
在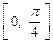 上为单调递增,则
上为单调递增,则
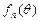 的最大值为
的最大值为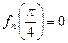 ,最小值为
,最小值为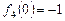 . …… 11分
. …… 11分
当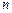 为偶数时,一方面有
为偶数时,一方面有 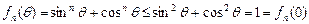 .
.
另一方面,由于对任意正整数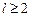 ,有
,有
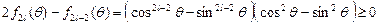 ,
,
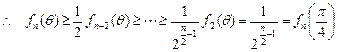 .
.
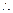 函数
函数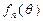 的最大值为
的最大值为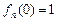 ,最小值为
,最小值为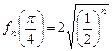 .
.
综上所述,当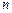 为奇数时,函数
为奇数时,函数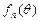 的最大值为
的最大值为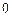 ,最小值为
,最小值为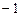 .
.
当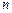 为偶数时,函数
为偶数时,函数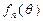 的最大值为
的最大值为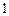 ,最小值为
,最小值为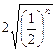 . …… 13分
. …… 13分
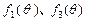 在
在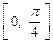 上均为单调递增的函数. 1分
上均为单调递增的函数. 1分对于函数
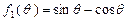 ,设
,设 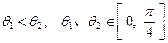 ,则
,则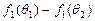
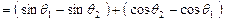 ,
,
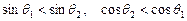 ,
,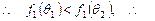 函数
函数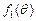 在
在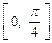 上单调递增. 3分
上单调递增. 3分(2)
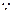 原式左边
原式左边 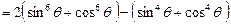
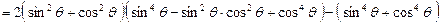
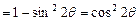 .… 5分
.… 5分又
 原式右边
原式右边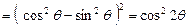 .
. 
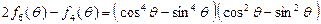 . 6分
. 6分(3)当
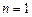 时,函数
时,函数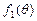 在
在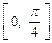 上单调递增,
上单调递增,
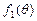 的最大值为
的最大值为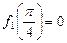 ,最小值为
,最小值为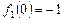 .
. 当
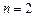 时,
时,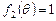 ,
,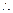 函数
函数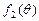 的最大、最小值均为1.
的最大、最小值均为1.当
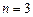 时,函数
时,函数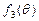 在
在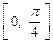 上为单调递增.
上为单调递增.
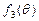 的最大值为
的最大值为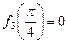 ,最小值为
,最小值为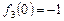 .
.当
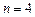 时,函数
时,函数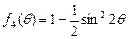 在
在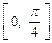 上单调递减,
上单调递减,
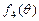 的最大值为
的最大值为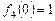 ,最小值为
,最小值为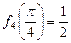 . … 9分
. … 9分下面讨论正整数
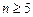 的情形:
的情形:当
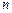 为奇数时,对任意
为奇数时,对任意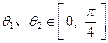 且
且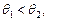
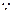
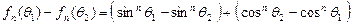 ,
,以及
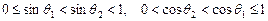 ,
,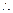
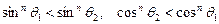 ,从而
,从而 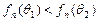 .
.
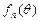 在
在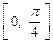 上为单调递增,则
上为单调递增,则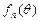 的最大值为
的最大值为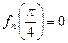 ,最小值为
,最小值为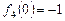 . …… 11分
. …… 11分当
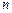 为偶数时,一方面有
为偶数时,一方面有 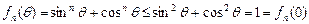 .
.另一方面,由于对任意正整数
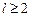 ,有
,有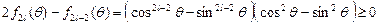 ,
,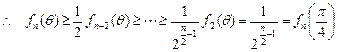 .
.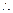 函数
函数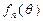 的最大值为
的最大值为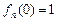 ,最小值为
,最小值为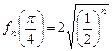 .
. 综上所述,当
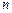 为奇数时,函数
为奇数时,函数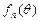 的最大值为
的最大值为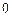 ,最小值为
,最小值为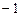 .
.当
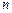 为偶数时,函数
为偶数时,函数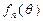 的最大值为
的最大值为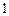 ,最小值为
,最小值为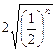 . …… 13分
. …… 13分
练习册系列答案
相关题目
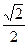 , 求
, 求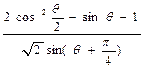 的值.
的值.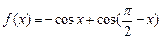 ,
,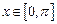 ,求函数
,求函数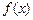 的最大值与最小值及此时x的值;
的最大值与最小值及此时x的值;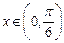 ,且
,且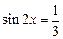 ,求
,求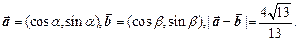
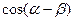 的值; (2)若
的值; (2)若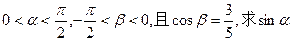 的值。
的值。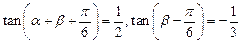 ,则
,则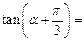
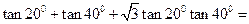 _____________。
_____________。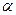 =4,cot
=4,cot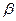 =
=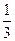 ,则tan(
,则tan(



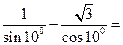 ___ _______.
___ _______.