题目内容
如图,在△ABC中,∠CAB=∠CBA=30°,AC、BC边上的高分别为BD、AE,
则以A、B为焦点,且过D、E的椭圆与双曲线的离心率的倒数和为 ( ) 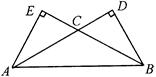
A. B.1 C.2
B.1 C.2 D.2
D.2
A
解析试题分析:根据题意,设AB=2c,则AE=BD=c,BE=AD= c ,∴在以A,B为焦点,且过D,E的椭圆中,离心率=
c ,∴在以A,B为焦点,且过D,E的椭圆中,离心率=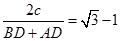 ,以A,B为焦点,且过D,E的双曲线中,离心率=
,以A,B为焦点,且过D,E的双曲线中,离心率=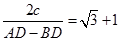 ,椭圆与双曲线的离心率的倒数和为:
,椭圆与双曲线的离心率的倒数和为: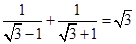 ,故选A
,故选A
考点:本题考查了双曲线的性质和应用
点评:解题时要认真审题,注意公式的灵活运用

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
如图所示,在 中,
中, ,
, ,高
,高 ,在
,在 内作射线
内作射线 交
交 于点
于点 ,则
,则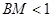 的概率为( )
的概率为( )
A. | B. | C. | D. |
已知 △
△ 中,
中, 以
以 为直径的圆交
为直径的圆交 于
于 ,则
,则 的长为( )
的长为( )
A. | B. | C. | D. |
下列说法中正确的个数是
①垂直于半径的直线是圆的切线;
②过圆心且垂直于切线的直线必过切点;
③过切点且垂直于切线的直线必过圆心;
④过半径的一端且垂直于这条半径的直线是圆的切线;
⑤同心圆内大圆的弦AB是小圆的切线,则切点是AB的中点.
| A.2 | B.3 | C.4 | D.5 |
如图所示,AD是△ABC的中线,E是CA边的三等分点,BE交AD于点F,则AF∶FD为
| A.2∶1 | B.3∶1 |
| C.4∶1 | D.5∶1 |
如图,设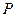 为
为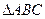 内一点,且
内一点,且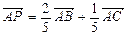 ,则
,则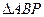 的面积与
的面积与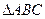 的
的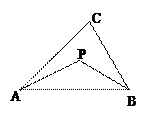 面积之比等于( ).
面积之比等于( ).
A.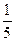 | B.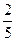 |
C.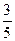 | D.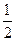 |

 是半径等于
是半径等于 的圆
的圆 的直径,
的直径, 是圆
是圆 ,
, ,若
,若 ,
,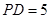 ,则
,则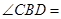 .
.

 。若
。若 EF到CD与AB的距离之比为
EF到CD与AB的距离之比为 ,则可推算出:
,则可推算出: ,用类比的方法,推想出下列问题的结果,在上面的梯形ABCD中,延长梯形的两腰AD和BC交于O点,设
,用类比的方法,推想出下列问题的结果,在上面的梯形ABCD中,延长梯形的两腰AD和BC交于O点,设 ,
, 的面积分别为
的面积分别为 ,EF//AB,且EF到CD与AB的距离之比为
,EF//AB,且EF到CD与AB的距离之比为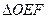 的面积
的面积 与
与
 B
B 
 D
D