题目内容
18.已知A(3,3),B(-1,-5),过线段AB的中点且斜率为-1的直线的方程是( )| A. | y-1=-(x-1) | B. | y-1=-(1-x) | C. | y+1=-(x-1) | D. | y+1=-(x+1) |
分析 根据中点坐标公式,求出线段AB的中点,再根据点斜式得到直线方程.
解答 解:∵A(3,3),B(-1,-5),
∴线段AB的中点坐标为($\frac{3-1}{2}$,$\frac{3-5}{2}$),即(1,-1),
∵过线段AB的中点且斜率为-1,
∴直线的方程为y+1=-(x-1),
故选:C.
点评 本题考查了直线方程的求法,关键是掌握中点坐标公式.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
9.过曲线C:y=$\frac{1}{x}$(x>0)上一点P(x0,y0)作曲线C的切线,若切线的斜率为-4,则x0等于( )
| A. | 2 | B. | $\frac{1}{2}$ | C. | 4 | D. | $\frac{1}{4}$ |
6.在等比数列{an}(n∈N*)中,若a1=1,a4=$\frac{1}{8}$,则该数列的前10项和为( )
| A. | 2-$\frac{1}{2^4}$ | B. | 2-$\frac{1}{{2}^{9}}$ | C. | 2-$\frac{1}{{{2^{10}}}}$ | D. | 2-$\frac{1}{{{2^{11}}}}$ |
10.设$\overrightarrow{e_1},\overrightarrow{e_2}$为两不共线的向量,则$\overrightarrow a=\overrightarrow{e_1}+λ\overrightarrow{e_2}$与$\overrightarrow b=-({2\overrightarrow{e_2}-3\overrightarrow{e_1}})$共线的条件是( )
| A. | λ=$\frac{3}{2}$ | B. | λ=$\frac{2}{3}$ | C. | λ=-$\frac{2}{3}$ | D. | λ=-$\frac{3}{2}$ |
7.下列幂函数中,过点(0,0),(1,1)的偶函数是( )
| A. | y=x${\;}^{\frac{1}{2}}$ | B. | y=x${\;}^{\frac{1}{3}}$ | C. | y=x-2 | D. | y=x4 |

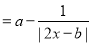 是偶函数,
是偶函数, 为实常数.
为实常数.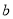 的值;
的值; 时,是否存在
时,是否存在 ,使得函数
,使得函数 在区间
在区间 上的函数值组成的集合也是
上的函数值组成的集合也是 ,若存在,求出
,若存在,求出 ,
, 的值;否则,说明理由.
的值;否则,说明理由.