题目内容
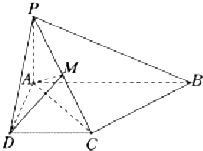
【题目】如图，将绘有函数f（x）=2sin（ωx+φ）（ω＞0， 
＜φ＜π）部分图象的纸片沿x轴折成直二面角，若AB之间的空间距离为 
，则f（﹣1）=（ ） 
A.﹣2
B.2
C.- 
D.
【答案】B
【解析】解：由函数的图象可得2sinφ=1，可得sinφ= 
，再根据 
＜φ＜π，可得φ= 
．
再根据A、B两点之间的距离为 
= 
，求得T=6，
再根据T= 
=6，求得ω= 
．
∴f（x）=2sin（ x+ ），f（﹣1）=2sin（﹣ + ）=2，
故选：B．
根据图象过点（0，1），结合φ的范围求得φ的值，再根据A、B两点之间的距离为 = ，求得T的值，可得ω的值，从而求得函数的解析式，从而求得f（﹣1）的值．
练习册系列答案
相关题目
【题目】某险种的基本保费为
（单位：元），继续购买该险种的投保人称为续保人，
续保人本年度的保费与其上年度出险次数的关联如下：
上年度出险次数 | 0 | 1 | 2 | 3 | 4 |
|
保费 |
|
|
|
|
|
|
随机调查了该险种的400名续保人在一年内的出险情况，得到如下统计表：
出险次数 | 0 | 1 | 2 | 3 | 4 |
|
频数 | 120 | 100 | 60 | 60 | 40 | 20 |
（Ⅰ）记A为事件：“一续保人本年度的保费不高于基本保费”.求
的估计值；
（Ⅱ）记B为事件：“一续保人本年度的保费高于基本保费但不高于基本保费的190％”.
求
的估计值；
（III）求续保人本年度的平均保费估计值.
