题目内容
设函数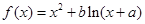 ,其中
,其中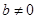 。
。
(1)当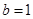 时,
时,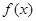 在
在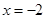 时取得极值,求
时取得极值,求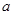 ;
;
(2)当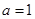 时,若
时,若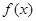 在
在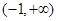 上单调递增,求
上单调递增,求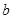 的取值范围;
的取值范围;
(3)证明对任意的正整数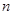 ,不等式
,不等式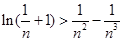 都成立。
都成立。
【答案】
解:(1) 当 时,
时, ,依题意有
,依题意有 ,故
,故 (3分)
(3分)
(2)当 时,
时,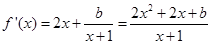 ,若
,若 在
在 上单调递增,则
上单调递增,则
设 ,
, (7分)
(7分)
(3) 若证不等式 ,设
,设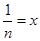 ,
,
可证当 时,
时,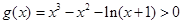 恒成立,
恒成立,
 在
在 上恒正,
上恒正,
 在
在 上单调递增,当
上单调递增,当 时,恒有
时,恒有
即当 时,有
时,有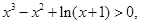

故对任意正整数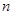 ,不等式
,不等式 成立。
成立。
【解析】略

练习册系列答案
相关题目
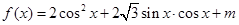 .其中
.其中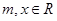
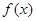 的最小正周期;
的最小正周期;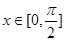 时,求实数
时,求实数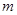 的值,使函数
的值,使函数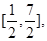 并求此时
并求此时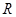 上的对称中心.
上的对称中心.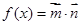 ,其中向量
,其中向量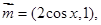
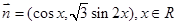
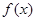 的最小正周期;
的最小正周期;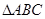 中,
中, 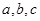 分别是角
分别是角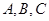 的对边,
的对边, 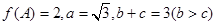 求
求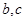 的值.
的值.