题目内容
设函数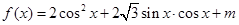 .其中
.其中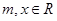
(1)求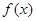 的最小正周期;
的最小正周期;
(2)当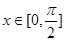 时,求实数
时,求实数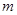 的值,使函数
的值,使函数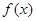 的值域恰为
的值域恰为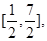 并求此时
并求此时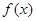 在
在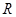 上的对称中心.
上的对称中心.
【答案】
(1)最小正周期T=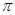 ;(2)
;(2)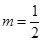 ,对称中心为
,对称中心为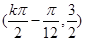 .
.
【解析】
试题分析:(1)将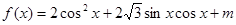 降次化一得
降次化一得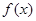
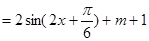 由此可得函数
由此可得函数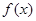 的最小正周期;(2)
的最小正周期;(2)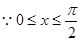 ,
,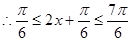 ,从而可得
,从而可得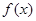 的值域,再由题设告知
的值域,再由题设告知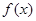 的值域恰为
的值域恰为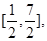 这样可得
这样可得 的值;再结合
的值;再结合 的对称中心可求得
的对称中心可求得 在
在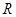 上的对称中心.
上的对称中心.
试题解析:(1)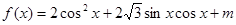
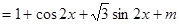
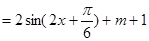 4分
4分
∴函数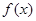 的最小正周期T=
的最小正周期T=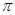 .
5分
.
5分
(2)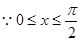
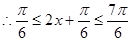
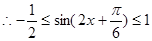
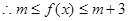 又
又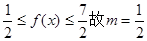 , 8分
, 8分
令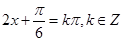 ,解得
,解得 ,对称中心为
,对称中心为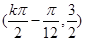 . 12分
. 12分
考点:1、三角恒等变换;2、三角函数的周期、值域及对称中心.

练习册系列答案
相关题目
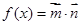 ,其中向量
,其中向量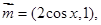
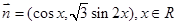
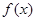 的最小正周期;
的最小正周期;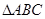 中,
中, 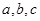 分别是角
分别是角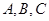 的对边,
的对边, 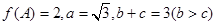 求
求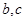 的值.
的值. 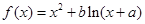 ,其中
,其中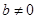 。
。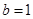 时,
时,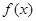 在
在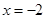 时取得极值,求
时取得极值,求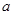 ;
;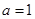 时,若
时,若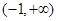 上单调递增,求
上单调递增,求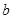 的取值范围;
的取值范围;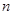 ,不等式
,不等式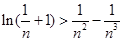 都成立。
都成立。