有一塔形几何体由若干个正方体构成.构成方式如右图所示.上层正方体下底面的四个顶点是下层正方体上底面各边的中点.已知最底层正方体的棱长为2,且该塔形的表面积(含最底层正方体的底面面积)超过39,则该塔形中正方体的个数至少是A.4 B.5 C.6 D.7 题目和参考答案——青夏教育精英家教网—

题目内容

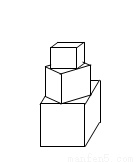
有一塔形几何体由若干个正方体构成，构成方式如右图所示，上层正方体下底面的四个顶点是下层正方体上底面各边的中点.已知最底层正方体的棱长为2,且该塔形的表面积(含最底层正方体的底面面积)超过39,则该塔形中正方体的个数至少是（）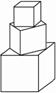

A.4 B.5 C.6 D.7

试题答案

相关练习册答案

解析:依题可知:S_表=2S_下底+S_侧

=2×2²+4［2²+()²+1²+…+2^3-n］

=8+4·＞39.

从而得n=6.

答案：C

练习册系列答案

考出好成绩系列答案

相关题目

A.4 B.5

C.6 D.7

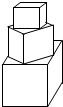有一塔形几何体由若干个正方体构成，构成方式如图所示，上层正方体下底面的四个顶点是下层正方体上底面各边的中点。已知最底层正方体的棱长为2，且该塔形的表面积(含最底层正方体的底面面积)超过39，则该塔形中正方体的个数至少是 ( )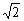

A 4；

B 5；

C 6；

D 7；

有一塔形几何体由若干个正方体构成，构成方式如图所示，上层正方体下底面的四个顶点是下层正方体上底面各边的中点.已知最底层正方体的棱长为2，且该塔形的表面积(含最底层正方体的底面面积)超过39，则该塔形中正方体的个数至少是___________.

试题分类