Question

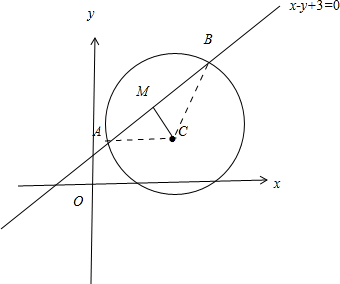
（2012•自贡三模）已知圆C：（x-a）²+（y-2）²=4（a＞0）及直线l：x-y+3=0，当直线l被C截得弦长为2

3

时，则a=

2

-1

．

Answer 1

分析：由题意可得圆心C（a，2）半径r=2，则圆心（a，2）到直线x-y+3=0得距离d=

|a-2+3|

2

=

|a+1|

2

，在Rt△CBM中由勾股定理可得，d²+BM²=BC²结合a＞0可求

解答：解：由题意可得圆心C（a，2）半径r=2
则圆心（a，2）到直线x-y+3=0的距离d=

|a-2+3|

2

=

|a+1|

2

Rt△CBM中由勾股定理可得，d²+BM²=BC²

(a+1)2

2

+3=4
∵a＞0
∴a=

2

-1或a=-

2

-1（舍去）
故答案为：

2

-1

点评：本题主要考查了直线与圆相交的 弦的应用，出了此类问题一般有两个方法：①直接利用弦长公式求解，该方法思路清晰但需要一定的计算②利用本题中的解法，结合弦长及弦心距及半径三者之间的关系进行求解．