题目内容
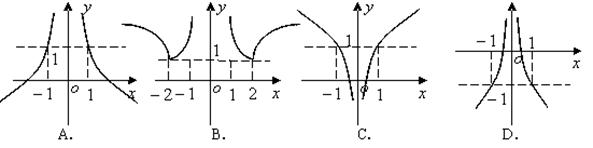
设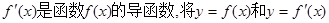 的图象画在同一个直角坐标系中,不可能正确的是( )
的图象画在同一个直角坐标系中,不可能正确的是( )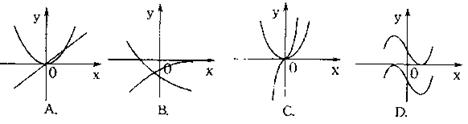
D.
解析试题分析:A选项中像二次函数图像的当做导函数,则可知导函数的值大于或等于零,所以原函数函数是递增的.即A选项正确.B选项把递增的那支作为导函数可知,导函数小于零,所以原函数的递减.所以B选项正确.选项C类似选项A.对于选项D.若x轴上方的做导函数,则可知导函数大于或等于零,所以原函数递增.即另一只不符合.若x轴下方的为导函数则可知,导函数小于或等于零,所以原函数递减.另一只也不符合.故选D.本题考察的知识点是学会看懂导函数图像.关注导函数的正负与函数的单调性的关系.
考点:1.导函数图像的正负的含义.2.函数的单调性的判断方法.3.观察图像能力.

练习册系列答案
相关题目
对于定义在R上的奇函数
| A.0 | B.—1 | C.3 | D.2 |
下列函数中,在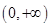 上为增函数的是 ( )
上为增函数的是 ( )
A.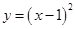 | B.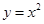 | C.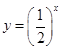 | D.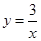 |
已知函数f(x)=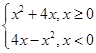 若f(2-a2)>f(a),则实数a的取值范围是( )
若f(2-a2)>f(a),则实数a的取值范围是( )
| A.(-∞,-1)∪(2,+∞) | B.(-1,2) |
| C.(-2,1) | D.(-∞,-2)∪(1,+∞) |
函数 的单调递增区间是( )
的单调递增区间是( )
A.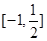 | B.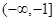 | C.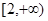 | D.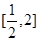 |
函数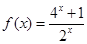 的图象( )
的图象( )
| A.关于原点对称 | B.关于直线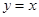 对称 对称 |
C.关于 轴对称 轴对称 | D.关于 轴对称 轴对称 |
已知奇函数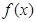 在
在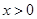 时,
时,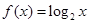 ,则
,则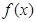 在区间
在区间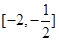 的值域为( )
的值域为( )
A.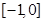 | B.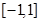 | C.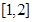 | D.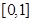 |
函数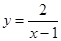 的定义域是
的定义域是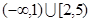 ,则其值域为( )
,则其值域为( )
A.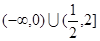 | B.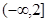 |
C.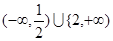 | D. |
 ,
, 的图象大致为下图的( )
的图象大致为下图的( )