题目内容
设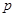 ∶
∶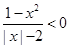 ,
, ∶
∶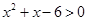 ,则
,则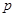 是
是 的
的
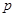 ∶
∶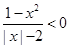 ,
, ∶
∶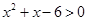 ,则
,则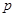 是
是 的
的| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
B
本题考查不等式的解法以及充要条件的判断
由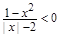 得
得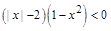 ,即
,即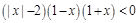 ①
①
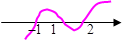 当
当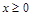 时,不等式 ①可化为
时,不等式 ①可化为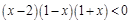 ,即
,即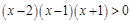 ,由序轴标根法得
,由序轴标根法得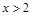 或
或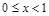 ;
;
 当
当 时,不等式 ①可化为
时,不等式 ①可化为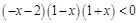 ,即
,即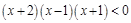 ,由序轴标根法得
,由序轴标根法得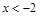 或
或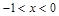 ;
;
即不等式①的解集为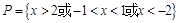
所以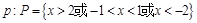
又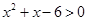 得
得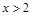 或
或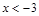 ,即
,即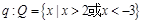
则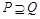 且
且 ,即
,即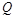 是
是 的真子集,所以
的真子集,所以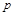 是
是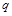 的必要不充分条件.
的必要不充分条件.
正确答案为B
由
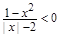 得
得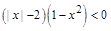 ,即
,即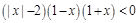 ①
①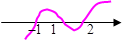 当
当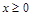 时,不等式 ①可化为
时,不等式 ①可化为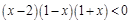 ,即
,即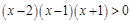 ,由序轴标根法得
,由序轴标根法得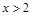 或
或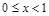 ;
; 当
当 时,不等式 ①可化为
时,不等式 ①可化为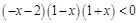 ,即
,即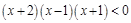 ,由序轴标根法得
,由序轴标根法得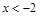 或
或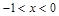 ;
;即不等式①的解集为
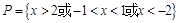
所以
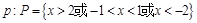
又
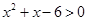 得
得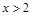 或
或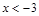 ,即
,即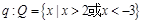
则
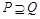 且
且 ,即
,即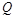 是
是 的真子集,所以
的真子集,所以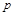 是
是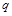 的必要不充分条件.
的必要不充分条件.正确答案为B

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
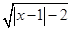 的定义域是(-∞,-1)∪[3,+∞],则 ( )
的定义域是(-∞,-1)∪[3,+∞],则 ( )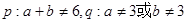 ,则
,则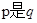 的( )条件
的( )条件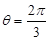 ”是”
”是”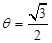 ”的 ( )
”的 ( )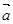 与
与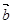 -
-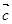 都是非零向量,则“
都是非零向量,则“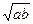 (G≠0)是a,G,b成等比数列的充分非必要条件;②若角α,β满足cosαcosβ=1,则sin(α+β)=0;③若不等式|x-4|+|x-3|<a的解集非空,则必有a≥1;④函数y=sinx+sin|x|的值域是[-2,2].
(G≠0)是a,G,b成等比数列的充分非必要条件;②若角α,β满足cosαcosβ=1,则sin(α+β)=0;③若不等式|x-4|+|x-3|<a的解集非空,则必有a≥1;④函数y=sinx+sin|x|的值域是[-2,2].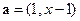 ,
,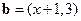 ,则
,则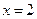
 是
是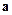 ∥
∥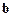 的
的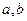 ,
,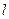 表示不同的直线,
表示不同的直线,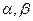 表示两个不同的平面,给出如下四组命题:
表示两个不同的平面,给出如下四组命题: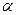 ”的充要条件是“直线
”的充要条件是“直线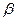 ”的必要非充分条件是“存在
”的必要非充分条件是“存在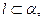
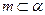 且
且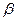 ,
, ∥
∥