题目内容
如果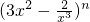 的展开式中含有非零常数项,则正整数n的最小值为
的展开式中含有非零常数项,则正整数n的最小值为
- A.3
- B.5
- C.6
- D.10
B
分析:利用二项展开式的通项公式求出第r+1项,令x的指数为0得方程,求使方程有整数解的最小n值即可.
解答:由展开式通项有 =Cnr•3n-r•(-2)r•x2n-5r
=Cnr•3n-r•(-2)r•x2n-5r
由题意得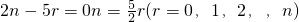 ,
,
故当r=2时,正整数n的最小值为5,
故选项为B
点评:本题主要考查二项式定理的基本知识,以通项公式切入探索,由整数的运算性质易得所求.本题中“非零常数项”为干扰条件.
分析:利用二项展开式的通项公式求出第r+1项,令x的指数为0得方程,求使方程有整数解的最小n值即可.
解答:由展开式通项有
 =Cnr•3n-r•(-2)r•x2n-5r
=Cnr•3n-r•(-2)r•x2n-5r由题意得
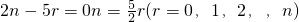 ,
,故当r=2时,正整数n的最小值为5,
故选项为B
点评:本题主要考查二项式定理的基本知识,以通项公式切入探索,由整数的运算性质易得所求.本题中“非零常数项”为干扰条件.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

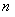
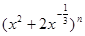 的展开式中含有非零常数项,则正整数
的展开式中含有非零常数项,则正整数 的最小值为( )
的最小值为( )