题目内容
(2012•湛江二模)对一个定义在R上的函数f(x)有以下四种说法:
①?x∈R,f(1-x)=f(1+x);
②在区间(-∞,0)上单调递减;
③对任意x1>x2>0满足f(x1)>f(x2);
④是奇函数.
则以上说法中能同时成立的最多有( )
①?x∈R,f(1-x)=f(1+x);
②在区间(-∞,0)上单调递减;
③对任意x1>x2>0满足f(x1)>f(x2);
④是奇函数.
则以上说法中能同时成立的最多有( )
分析:分析①?x∈R,f(1-x)=f(1+x),关于x=1对称;对于②f(x)在区间(-∞,0)上单调递减;①②可以在一起;③表示其为增函数,④为奇函数,故③④可以放在一起;
解答:解:①?x∈R,f(1-x)=f(1+x),对称轴x=
=1,若其在(-∞,0)上单调递减,
在(1,+∞)上单调递减,所以①不能与③④一起成立,
③对任意x1>x2>0满足f(x1)>f(x2),f(x)在(0,+∞)上单调递增,
④f(x)为奇函数,不能与①一起成立,可以与③一起成立,
∴①②可以一起成立,③④可以一起成立,
故选B.
| 1-x+1+x |
| 2 |
在(1,+∞)上单调递减,所以①不能与③④一起成立,
③对任意x1>x2>0满足f(x1)>f(x2),f(x)在(0,+∞)上单调递增,
④f(x)为奇函数,不能与①一起成立,可以与③一起成立,
∴①②可以一起成立,③④可以一起成立,
故选B.
点评:此题主要考查函数奇偶性的定义及其性质,利用函数的对称轴和单调性进行判断,此题是一道好题;

练习册系列答案
相关题目
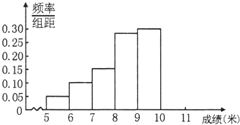 (2012•湛江二模)某市为了解今年高中毕业生的身体素质状况,从本市某校高中毕业班中抽取一个班进行实心球测试,成绩在8米及以上的为合格.把所得数据进行整理后,分成6组画出频率分布直方图的一部分(如图),已知第一小组为[5,6),从左到右前5个小组的频率分别为0.06,0.10,0.14,0.28,0.30.第6小组的频数是6.
(2012•湛江二模)某市为了解今年高中毕业生的身体素质状况,从本市某校高中毕业班中抽取一个班进行实心球测试,成绩在8米及以上的为合格.把所得数据进行整理后,分成6组画出频率分布直方图的一部分(如图),已知第一小组为[5,6),从左到右前5个小组的频率分别为0.06,0.10,0.14,0.28,0.30.第6小组的频数是6. (2012•湛江二模)运行如图所示框图,坐标满足不等式组
(2012•湛江二模)运行如图所示框图,坐标满足不等式组 (2012•湛江二模)如图,Rt△ABC中,∠C=90°,∠A=30°,圆O经过B、C且与AB、AC分别相交于D、E.若AE=EC=
(2012•湛江二模)如图,Rt△ABC中,∠C=90°,∠A=30°,圆O经过B、C且与AB、AC分别相交于D、E.若AE=EC=