题目内容
把正方形ABCD沿对角线BD折成直二面角，则AB与平面BCD所成角为
45°
45°
．分析：取BD的中点E，则AE⊥BD，可得AE⊥平面BCD，故∠ABD为AB与面BCD所成的角，即可求得结论．
解答：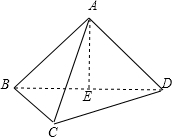
解：取BD的中点E，则AE⊥BD，
∵平面ABD∩平面BCD=BD，平面ABD⊥平面BCD
∴AE⊥平面BCD
∴∠ABD为AB与面BCD所成的角，
∵△ABD为等腰直角三角形
∴∠ABD=45°
故答案为：45°
解：取BD的中点E，则AE⊥BD，∵平面ABD∩平面BCD=BD，平面ABD⊥平面BCD
∴AE⊥平面BCD
∴∠ABD为AB与面BCD所成的角，
∵△ABD为等腰直角三角形
∴∠ABD=45°
故答案为：45°
点评：本题考查平面图形的翻折，考查线面角，考查学生的计算能力，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
把正方形ABCD沿对角线AC折起，当以A、B、C、D四点为顶点的三棱锥体积最大时，直线BD和平面ABC所成的角的大小为（ ）
| A、90° | B、60° | C、45° | D、30° |
8、如图把正方形ABCD沿对角线BD折成直二面角，对于下面结论：