题目内容
如图所示,点N在圆x2+y2=4上运动,DN⊥x轴,点M在DN的延长线上,且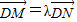 (λ>0).
(λ>0).(1)求点M的轨迹方程,并求当λ为何值时M的轨迹表示焦点在x轴上的椭圆;
(2)当
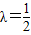 时,(1)所得曲线记为C,已知直线
时,(1)所得曲线记为C,已知直线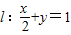 ,P是l上的动点,射线OP(O为坐标原点)交曲线C于点R,又点Q在OP上且满足|OQ|•|OP|=|OR|2,求点Q的轨迹方程.
,P是l上的动点,射线OP(O为坐标原点)交曲线C于点R,又点Q在OP上且满足|OQ|•|OP|=|OR|2,求点Q的轨迹方程.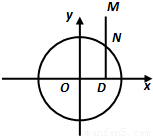
【答案】分析:(1)利用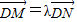 ,确定动点坐标之间的关系,利用点N在圆x2+y2=4上运动,可以得到点M的轨迹方程,从而可得λ为何值时M的轨迹表示焦点在x轴上的椭圆;
,确定动点坐标之间的关系,利用点N在圆x2+y2=4上运动,可以得到点M的轨迹方程,从而可得λ为何值时M的轨迹表示焦点在x轴上的椭圆;
(2)设P(x1,y1),R(x2,y2),Q(x,y),根据比例性质,条件|OQ|•|OP|=|OR|2,可得坐标之间的关系,化简变形即可得到点Q的轨迹方程.
解答: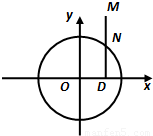 解:(1)设M(x,y),N(x,y),
解:(1)设M(x,y),N(x,y),
由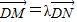 得 x=x,y=λy,
得 x=x,y=λy,
∴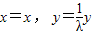 ,…(2分)
,…(2分)
把N(x,y)代入圆的方程得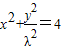 ,
,
化简得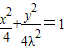 .…(4分)
.…(4分)
当0<λ<1时,M的轨迹表示焦点在x轴上的椭圆.…(5分)
(2))当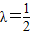 时,(1)所得曲线C为
时,(1)所得曲线C为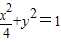 .
.
设P(x1,y1),R(x2,y2),Q(x,y)
∵P在l上、R在椭圆上,∴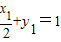 ①
①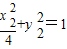 ②…(7分)
②…(7分)
设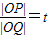 ,由比例性质得
,由比例性质得 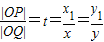 ,∴x1=tx,y1=ty,…(8分)
,∴x1=tx,y1=ty,…(8分)
代入①得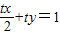 ③…(9分)
③…(9分)
∵|OQ|•|OP|=|OR|2,∴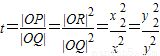 ,
,
∴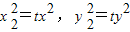 …(10分)
…(10分)
代入②得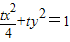 ④…(11分)
④…(11分)
由③④联立得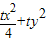 =
=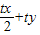 ,又t≠0,
,又t≠0,
∴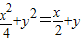 ,原点除外.
,原点除外.
化简得点Q的轨迹方程为x2-2x+4y2-4y=0(原点除外).…(13分)
点评:本题重点考查代入法求轨迹方程,考查消参思想,解题的关键是确定动点坐标之间的关系,综合性较强.
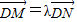 ,确定动点坐标之间的关系,利用点N在圆x2+y2=4上运动,可以得到点M的轨迹方程,从而可得λ为何值时M的轨迹表示焦点在x轴上的椭圆;
,确定动点坐标之间的关系,利用点N在圆x2+y2=4上运动,可以得到点M的轨迹方程,从而可得λ为何值时M的轨迹表示焦点在x轴上的椭圆;(2)设P(x1,y1),R(x2,y2),Q(x,y),根据比例性质,条件|OQ|•|OP|=|OR|2,可得坐标之间的关系,化简变形即可得到点Q的轨迹方程.
解答:
 解:(1)设M(x,y),N(x,y),
解:(1)设M(x,y),N(x,y),由
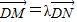 得 x=x,y=λy,
得 x=x,y=λy,∴
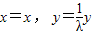 ,…(2分)
,…(2分)把N(x,y)代入圆的方程得
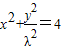 ,
,化简得
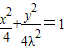 .…(4分)
.…(4分)当0<λ<1时,M的轨迹表示焦点在x轴上的椭圆.…(5分)
(2))当
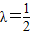 时,(1)所得曲线C为
时,(1)所得曲线C为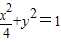 .
.设P(x1,y1),R(x2,y2),Q(x,y)
∵P在l上、R在椭圆上,∴
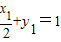 ①
①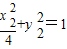 ②…(7分)
②…(7分)设
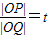 ,由比例性质得
,由比例性质得 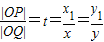 ,∴x1=tx,y1=ty,…(8分)
,∴x1=tx,y1=ty,…(8分)代入①得
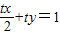 ③…(9分)
③…(9分)∵|OQ|•|OP|=|OR|2,∴
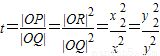 ,
,∴
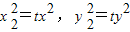 …(10分)
…(10分)代入②得
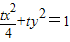 ④…(11分)
④…(11分)由③④联立得
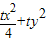 =
=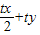 ,又t≠0,
,又t≠0,∴
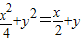 ,原点除外.
,原点除外.化简得点Q的轨迹方程为x2-2x+4y2-4y=0(原点除外).…(13分)
点评:本题重点考查代入法求轨迹方程,考查消参思想,解题的关键是确定动点坐标之间的关系,综合性较强.

练习册系列答案
相关题目
 如图所示,已知圆C:(x+1)2+y2=8,顶点A(1,0),M为圆上一动点,点P在AM上,点N在CM上,且满足
如图所示,已知圆C:(x+1)2+y2=8,顶点A(1,0),M为圆上一动点,点P在AM上,点N在CM上,且满足 如图所示,点N在圆x2+y2=4上运动,DN⊥x轴,点M在DN的延长线上,且
如图所示,点N在圆x2+y2=4上运动,DN⊥x轴,点M在DN的延长线上,且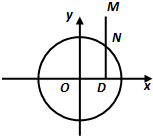 如图所示,点N在圆x2+y2=4上运动,DN⊥x轴,点M在DN的延长线上,且
如图所示,点N在圆x2+y2=4上运动,DN⊥x轴,点M在DN的延长线上,且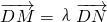 (λ>0).
(λ>0).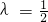 时,(1)所得曲线记为C,已知直线
时,(1)所得曲线记为C,已知直线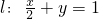 ,P是l上的动点,射线OP(O为坐标原点)交曲线C于点R,又点Q在OP上且满足|OQ|•|OP|=|OR|2,求点Q的轨迹方程.
,P是l上的动点,射线OP(O为坐标原点)交曲线C于点R,又点Q在OP上且满足|OQ|•|OP|=|OR|2,求点Q的轨迹方程. (λ>0),
(λ>0), 时,(1)所得曲线记为C,已知直线l:
时,(1)所得曲线记为C,已知直线l: +y=1,P是l上的动点,射线OP(O为坐标原点)交曲线C于点R,又点Q在OP上且满足|OQ|·|OP|=|OR|2,求点Q的轨迹方程。
+y=1,P是l上的动点,射线OP(O为坐标原点)交曲线C于点R,又点Q在OP上且满足|OQ|·|OP|=|OR|2,求点Q的轨迹方程。 