如图所示.已知圆C:(x+1)2+y2=8.顶点A(1.0).M为圆上一动点.点P在AM上.点N在CM上.且满足AM=2AP.NP•AM=0.点N的轨迹为曲线E．(1)求曲线E的方程,(2)过点A且倾斜角是45°的直线l交曲线E于两点H.Q.求|HQ|．题目和参考答案——青夏教育精英家教网—

题目内容

如图所示，已知圆C：（x+1）²+y²=8，顶点A（1，0），M为圆上一动点，点P在AM上，点N在CM上，且满足

，

•

=0，点N的轨迹为曲线E．
（1）求曲线E的方程；
（2）过点A且倾斜角是45°的直线l交曲线E于两点H、Q，求|HQ|．

分析：（1）利用线段垂直平分线的性质推出 NC+NM=r=2

＞AC，再利用椭圆的定义知，点N的轨迹是以A、C 为焦点的椭圆，利用待定系数法求出椭圆的方程．
（2）点斜式写出直线l方程，代入曲线E的方程，转化为一元二次方程，利用根与系数的关系和弦长公式求出|HQ|．

解答：解：（1）设点N的坐标为（x，y），∵

，∴点P为AM的中点，
∵

•

=0，∴NP⊥AM，∴NP是线段AM的垂直平分线，∴NM=NA，
又点N在CM上，设圆的半径是 r，则 r=2

，
∴NC=r-NM，∴NC+NM=NC+NA=r=2

＞AC，∴点N的轨迹是以A、C 为焦点的椭圆，
∵2a=2

，c=1，∴b=1，∴椭圆

+y²=1，即曲线E的方程：

+y²=1．
（2）∵过点A且倾斜角是45°的直线l交曲线E于两点H、Q，∴直线l方程为 y-0=x-1，
代入曲线E的方程得：3x²-4x=0，∴x₁+x₂=

，x₁•x₂=0，
由弦长公式得：|HQ|=

1+1

•

(x1+x2)2-4x1x2

，

点评：本题考查用定义法求轨迹方程，及直线与椭圆的位置关系，利用弦长公式求出弦长，属于中档题．

练习册系列答案

寒假创新型自主学习第三学期寒假衔接系列答案

相关题目

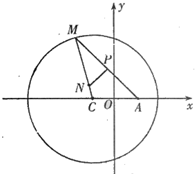如图所示，已知圆C：（x+1）²+y²=8，定点A（1，0），M为圆C上一动点，点P在线段AM上，点N在线段CM上，且满足

，

•

=0，点N的轨迹为曲线E．
（1）求曲线E的方程；
（2）若过定点F（0，2）的直线交曲线E于不同的两点G、H（点G在点F、H之间），且满足

=λ

，求λ的取值范围．

（理）如图所示，已知圆C：（x+1）²+y²=8，定点A（1，0），M为圆上一动点，点P在AM上，点N在CM上，且满足

，

•

=0，点N的轨迹为曲线E．
（1）求曲线E的方程；
（2）过点S（0，

）且斜率为k的动直线l交曲线E于A、B两点，在y轴上是否存在定点G，满足

使四边形NAPB为矩形？若存在，求出G的坐标和四边形NAPB面积的最大值；若不存在，说明理由．

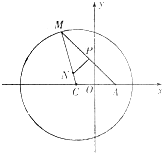如图所示，已知圆C：（x+1）²+y²=8，定点A（1，0），M为圆上一动点，点P在AM上，点N在CM上，且满足AM=2AP，NP⊥AM，点N的轨迹为曲线E．
（1）求曲线E的方程；
（2）若过定点F（0，2）的直线l交曲线E于不同的两点G、H（点G在点F、H之间），且满足FG=

FH，求直线l的方程；
（3）设曲线E的左右焦点为F₁，F₂，过F₁的直线交曲线于Q，S两点，过F₂的直线交曲线于R，T两点，且QS⊥RT，垂足为W；
（ⅰ）设W（x₀，y₀），证明：

＜1；
（ⅱ）求四边形QRST的面积的最小值．

（2006•石景山区一模）如图所示，已知圆C：（x+1）²+y²=8，定点A（1，0），M为圆上一动点，点P在AM上，点N在CM上，且满足

，

•

=0，点N的轨迹为曲线E．
（Ⅰ）求曲线E的方程；
（Ⅱ）若点B₁（x₁，y₁），B₂（-1，y₂），B₃（x₃，y₃）在曲线E上，线段B₁B₃的垂直平分线为直线l，且|B₁A|，|B₂A|，|B₃A|成等差数列，求x₁+x₃的值，并证明直线l过定点；
（Ⅲ）若过定点F（0，2）的直线交曲线E于不同的两点G、H（点G在点F、H之间），且满足

=λ

，求λ的取值范围．

如图所示，已知圆C：（x+1）²+y²=8，定点A（1，0），M为圆上一动点，点P在AM上，点N在CM上，且满足

试题分类