题目内容
若非零向量a,b满足|a|=|b|,(2a+b)·b=0,则a与b的夹角为( )
(A)30° (B)60° (C)120° (D)150°
【答案】
C
【解析】设a与b的夹角为θ,
则(2a+b)·b=2a·b+b2=2|a||b|cos θ+|b|2
=|b|2(2cos θ+1)=0,
又b为非零向量,∴2cos θ+1=0,
∴cos θ=- ,∴θ=120°.故选C.
,∴θ=120°.故选C.

练习册系列答案
相关题目
 R,
R, ”的否定是“
”的否定是“ ”;
”; ②若
②若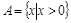 ,
, ,则
,则 ( RB)=A;
( RB)=A; 是偶函数的充要条件是
是偶函数的充要条件是 (
( Z);
Z); b,b=
b,b= R),则
R),则 .
.