题目内容
有下列命题:
①若非零向量
、
,满足
•
=0,则一定有
⊥
;
②将函数y=cos2x的图象向右平移
个单位,得到函数y=sin(2x-
)的图象;
③命题“若|x|≥2,则x≥2或x≤-2”的否命题是“若|x|≥2,则-2<x<2”;
④方程
+y2+Dx+Ey+F=0表示圆的充要条件是
+E2-4F≥0;
⑤对于命题p:?x∈R.使得x2+x+1<0,则¬p:?x∈R,均有x2+x+1≥0.
其中假命题的序号是
①若非零向量
| a |
| b |
| a |
| b |
| a |
| b |
②将函数y=cos2x的图象向右平移
| π |
| 3 |
| π |
| 6 |
③命题“若|x|≥2,则x≥2或x≤-2”的否命题是“若|x|≥2,则-2<x<2”;
④方程
| x | 2 |
| D | 2 |
⑤对于命题p:?x∈R.使得x2+x+1<0,则¬p:?x∈R,均有x2+x+1≥0.
其中假命题的序号是
③④
③④
.分析:①据课本必修4中的结论:非零向量
、
,若
•
=0,则一定有
⊥
.
②据平移变换的法则:“左加右减”可知,将函数y=cos2x的图象向右平移
个单位,得到函数y=cos[2(x-
)],再据诱导公式可进一步化出其表达式.
③命题“若p,则q”的否命题是“若¬p,则¬q”.据此可以判断出③的真假.
④将方程
+y2+Dx+Ey+F=0配方化为(x+
)2+(y+
)2=
,可以判断出④的真假.
⑤对于命题:“?x∈R,结论p成立”,则命题的否定是:“?x∈R,结论p的反面成立”据此可判断出其真假.
| a |
| b |
| a |
| b |
| a |
| b |
②据平移变换的法则:“左加右减”可知,将函数y=cos2x的图象向右平移
| π |
| 3 |
| π |
| 3 |
③命题“若p,则q”的否命题是“若¬p,则¬q”.据此可以判断出③的真假.
④将方程
| x | 2 |
| D |
| 2 |
| E |
| 2 |
| D2+E2-4F |
| 4 |
⑤对于命题:“?x∈R,结论p成立”,则命题的否定是:“?x∈R,结论p的反面成立”据此可判断出其真假.
解答:解:①非零向量
•
=0,则一定有
⊥
.
②将函数y=cos2x的图象向右平移
个单位,得到函数y=cos[2(x-
)]=cos(2x-
)=cos(
-2x)=cos[
-(2x-
)]=sin(2x-
)
的图象,故②正确.
③命题“若|x|≥2,则x≥2或x≤-2”的否命题应是“若|x|<2,则-2<x<2”,故③不正确.
④∵方程
+y2+Dx+Ey+F=0⇒(x+
)2+(y+
)2=
,
∴只有当
+E2-4F>0时,方程
+y2+Dx+Ey+F=0才表示一个圆,
因此④不正确.
⑤据命题:“?x∈R,结论p成立”,则命题的否定是:“?x∈R,结论p的反面成立”,
可知“命题p:?x∈R.使得x2+x+<0,则¬p:?x∈R,均有x2+x+1≥0”正确.
故答案为③④.
| a |
| b |
| a |
| b |
②将函数y=cos2x的图象向右平移
| π |
| 3 |
| π |
| 3 |
| 2π |
| 3 |
| 2π |
| 3 |
| π |
| 2 |
| π |
| 6 |
| π |
| 6 |
的图象,故②正确.
③命题“若|x|≥2,则x≥2或x≤-2”的否命题应是“若|x|<2,则-2<x<2”,故③不正确.
④∵方程
| x | 2 |
| D |
| 2 |
| E |
| 2 |
| D2+E2-4F |
| 4 |
∴只有当
| D | 2 |
| x | 2 |
因此④不正确.
⑤据命题:“?x∈R,结论p成立”,则命题的否定是:“?x∈R,结论p的反面成立”,
可知“命题p:?x∈R.使得x2+x+<0,则¬p:?x∈R,均有x2+x+1≥0”正确.
故答案为③④.
点评:本题综合考查了向量的数量积与垂直的关系、三角函数图象的变换与诱导公式、四种命题间的关系、圆的方程及命题的否定,解决问题的关键是掌握好有关基础知识及判断方法.

练习册系列答案
相关题目
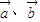 ,满足
,满足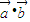 =0,则一定有
=0,则一定有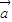 ⊥
⊥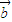 ;
;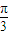 个单位,得到函数y=sin(2x-
个单位,得到函数y=sin(2x-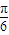 )的图象;
)的图象;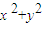 +Dx+Ey+F=0表示圆的充要条件是
+Dx+Ey+F=0表示圆的充要条件是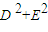 -4F≥0;
-4F≥0;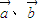 ,满足
,满足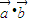 =0,则一定有
=0,则一定有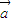 ⊥
⊥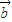 ;
;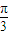 个单位,得到函数y=sin(2x-
个单位,得到函数y=sin(2x-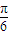 )的图象;
)的图象;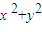 +Dx+Ey+F=0表示圆的充要条件是
+Dx+Ey+F=0表示圆的充要条件是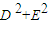 -4F≥0;
-4F≥0;