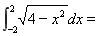题目内容
设f(x)=
x2-bx+c,不等式f(x)<0的解集是(-1,3),若f(7+|t|)>f(1+t2),求实数t的取值范围.
-3<t<3
【解析】∵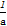
x2-bx+c<0的解集是(-1,3),
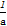∴>0且-1,3是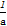x2-bx+c=0的两根,
∴
得
∵函数f(x)=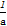x2-bx+c图象的对称轴方程为x=
=1,且f(x)在[1,+∞)上是增函数,
又∵7+|t|≥7>1,1+t2≥1,
则由f(7+|t|)>f(1+t2),得7+|t|>1+t2,
即|t|2-|t|-6<0,亦即(|t|+2)(|t|-3)<0,
∴|t|<3,即-3<t<3.
练习册系列答案
相关题目
通过随机询问110名性别不同的行人,对过马路是愿意走斑马线还是愿意走人行天桥进行抽样调查,得到如下的2×2列联表:
| 男 | 女 | 总计 |
走天桥 | 40 | 20 | 60 |
走斑马线 | 20 | 30 | 50 |
总计 | 60 | 50 | 110 |
由χ2=
算得,
χ2=
≈7.8.
以下结论正确的是( )
(A)有99%以上的把握认为“选择过马路的方式与性别有关”
(B)有99%以上的把握认为“选择过马路的方式与性别无关”
(C)在犯错误的概率不超过0.1%的前提下,认为“选择过马路的方式与性别有关”
(D)在犯错误的概率不超过0.1%的前提下,认为“选择过马路的方式与性别无关”
