题目内容
【题目】已知p:方程x2+mx+1=0有两个不等的负根;q:方程4x2+4(m﹣2)x+1=0无实根,若“p或q”真“p且q”为假,求m的取值范围.
【答案】解:若方程 x2+mx+1=0有两个不等的负根,
则 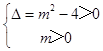
解得m>2,
若方程4x2+4(m﹣2)x+1=0无实根,则△=16(m﹣2)2﹣16<0,
解得:1<m<3
∵“p或q”真“p且q”,
因此,命题p,q应一真一假,
∴ ![]() 或
或 ![]() ,
,
解得:m∈(1,2]∪[3,+∞).
【解析】若“p或q”真“p且q”为假,命题p,q应一真一假,分类讨论,可得m的取值范围.
【考点精析】认真审题,首先需要了解命题的真假判断与应用(两个命题互为逆否命题,它们有相同的真假性;两个命题为互逆命题或互否命题,它们的真假性没有关系).

练习册系列答案
相关题目