题目内容
在平面直角坐标系中,从五个点:A(0,0)、B(2,0)、C(1,1)、D(0,2)、E(2,2)中任取三个,这三点能构成三角形的概率是________(结果用分数表示).
解:由题意可知AB=2,AC= 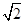 ,AD=2,AE="2"
,AD=2,AE="2" 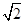 ,BC=
,BC= 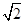 ,BD=2
,BD=2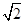 ,BE=2,CD=
,BE=2,CD=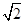 ,CE=
,CE= 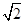 ,DE=2,
,DE=2,
任意三点组合有ABC,ABD,ABE,ACD,ACE,ADE,BCD,BCE,BDE,CDE,10种情况,
其中ABC,ABD,ABE,ACD,ADE,BCE,BDE,CDE能组成三角形,ACE,BCD不能组成三角形,
概率为8 /10 ="4/" 5 .
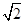 ,AD=2,AE="2"
,AD=2,AE="2" 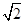 ,BC=
,BC= 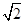 ,BD=2
,BD=2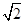 ,BE=2,CD=
,BE=2,CD=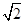 ,CE=
,CE= 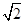 ,DE=2,
,DE=2,任意三点组合有ABC,ABD,ABE,ACD,ACE,ADE,BCD,BCE,BDE,CDE,10种情况,
其中ABC,ABD,ABE,ACD,ADE,BCE,BDE,CDE能组成三角形,ACE,BCD不能组成三角形,
概率为8 /10 ="4/" 5 .

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目




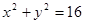 内的概率为 .
内的概率为 .
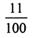
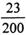
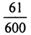
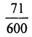
 ,则总体中的个体数为( )
,则总体中的个体数为( )


