题目内容
已知在△ABC中，C=2A，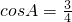
，且2
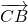=-27．
（1）求cosB的值；
（2）求AC的长度．
解：（1）∵C=2A，∴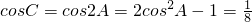
，
∴
，
∴
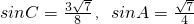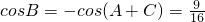．…（6分）
（2）∵C=2A，∴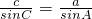
，∴
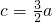． …（8分）
∵2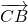=-27，
∴
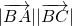=24，即 ac=24．
∴a2=16，c=6，
∴b=5，即 AC的长度为10．…（12分）
分析：（1）由条件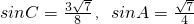，再由两角和差的余弦公式、诱导公式求得cosB=-cos（A+C）的值．
（2）由C=2A 利用正弦定理求得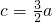．再由 2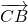=-27，求得 ac=24，由此可得 AC的长度（即b的值）．
点评：本题主要考查两角和差的正弦、二倍角公式、诱导公式、正弦定理的应用，两个向量的数量积的定义，属于中档题．
，∴
，∴
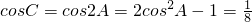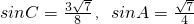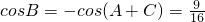．…（6分）（2）∵C=2A，∴
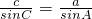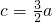，∴． …（8分）∵2
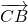=-27，∴
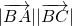=24，即 ac=24．∴a2=16，c=6，
∴b=5，即 AC的长度为10．…（12分）
分析：（1）由条件
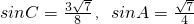，再由两角和差的余弦公式、诱导公式求得cosB=-cos（A+C）的值．（2）由C=2A 利用正弦定理求得
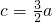．再由 2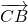=-27，求得 ac=24，由此可得 AC的长度（即b的值）．点评：本题主要考查两角和差的正弦、二倍角公式、诱导公式、正弦定理的应用，两个向量的数量积的定义，属于中档题．
练习册系列答案
考前必练系列答案
相关题目
（A）（不等式选讲）不等式log3（|x-4|+|x+5|）＞a对于一切x∈R恒成立，则实数a的取值范围是