题目内容
18.已知向量$\overrightarrow{a}$=m$\overrightarrow{i}$+5$\overrightarrow{j}$-$\overrightarrow{k}$,$\overrightarrow{b}$=3$\overrightarrow{i}$+$\overrightarrow{j}$+r$\overrightarrow{k}$若$\overrightarrow{a}$∥$\overrightarrow{b}$则实数m=15,r=-$\frac{1}{5}$.分析 由$\overrightarrow{a}$∥$\overrightarrow{b}$得出坐标对应成比例,分别求出实数m和r即可
解答 解:向量$\overrightarrow{a}$=m$\overrightarrow{i}$+5$\overrightarrow{j}$-$\overrightarrow{k}$=(m,5,-1),$\overrightarrow{b}$=3$\overrightarrow{i}$+$\overrightarrow{j}$+r$\overrightarrow{k}$=(3,1,r),$\overrightarrow{a}$∥$\overrightarrow{b}$,
则$\frac{m}{3}$=$\frac{5}{1}$=$\frac{-1}{r}$
解得m=15,r=-$\overline{5}$
故答案为:15,-$\frac{1}{5}$
点评 本题考点是空间共线向量的坐标表示,考查了空间共线向量等价条件的简单应用.

练习册系列答案
相关题目
8.已知全集U=R,集合A={1,2,3,4,5},B={x∈R|x>2},下图中阴影部分所表示的集合为( )
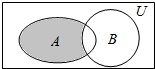

| A. | {1} | B. | {0,1} | C. | {1,2} | D. | {0,1,2} |
9.函数$y=2cos(\frac{π}{4}-2x)$的单调减区间是( )
| A. | $\{x|kπ+\frac{π}{8}≤x≤kπ+\frac{5π}{8},k∈Z\}$ | B. | {x|kπ-$\frac{3π}{8}$≤x≤kπ+$\frac{π}{8}$,k∈Z} | ||
| C. | {x|2kπ+$\frac{π}{8}$≤x≤2kπ+$\frac{5π}{8}$,k∈Z} | D. | {x|2kπ-$\frac{3π}{8}$≤x≤2kπ+$\frac{π}{8}$,k∈Z} |
6.复数z=4i2016-$\frac{5i}{1+2i}$(其中i为虚数单位)对应点在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
13.已知f(x)=|lnx|,设0<a<b,且f(a)=f(b),则a+2b的取值范围是( )
| A. | [3,+∞) | B. | (3,+∞) | C. | $[2\sqrt{2},+∞)$ | D. | $(2\sqrt{2},+∞)$ |
10.若双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>b>0)的渐近线和圆x2+y2-6y+8=0相切,则该双曲线的离心率等于( )
| A. | $\sqrt{2}$ | B. | 2 | C. | 3 | D. | $\sqrt{3}$ |