题目内容
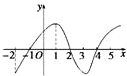
 14、如图是y=f(x)导数的图象,对于下列四个判断:
14、如图是y=f(x)导数的图象,对于下列四个判断:①f(x)在[-2,-1]上是增函数;
②x=-1是f(x)的极小值点;
③f(x)在[-1,2]上是增函数,在[2,4]上是减函数;
④x=3是f(x)的极小值点.
其中判断正确的是
②③
.分析:本题是一个图象题,考察两个知识点:一是导数的正负与函数单调性的关系,在某个区间上,导数为正,则函数在这个区间上是增函数,导数为负,则这个函数在这个区间上是减函数;二是极值判断方法,在导数为零的点处左增右减取到极大值,左减右增取到极小值.
解答:解:由图象可以看出,在[-2,-1]上导数小于零,故①不对;
x=-1左侧导数小于零,右侧导数大于零,所以x=-1是f(x)的极小值点,故②对;
在[-1,2]上导数大于零,在[2,4]上导数小于零,故③对;
x=3左右两侧导数的符号都为负,所以x=3不是极值点,④不对.
故答案为②③.
x=-1左侧导数小于零,右侧导数大于零,所以x=-1是f(x)的极小值点,故②对;
在[-1,2]上导数大于零,在[2,4]上导数小于零,故③对;
x=3左右两侧导数的符号都为负,所以x=3不是极值点,④不对.
故答案为②③.
点评:本题是较基础的知识型题,全面考查了用导数与单调性,导数与极值的关系,是知识性较强的一个题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
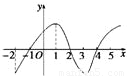 如图是y=f(x)导数的图象,对于下列四个判断:
如图是y=f(x)导数的图象,对于下列四个判断: 如图是y=f(x)导数的图象,对于下列四个判断:
如图是y=f(x)导数的图象,对于下列四个判断: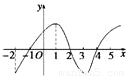 如图是y=f(x)导数的图象,对于下列四个判断:
如图是y=f(x)导数的图象,对于下列四个判断: