题目内容
已知:如图,在直角梯形ABCD中,AB∥CD,AD⊥AB,垂足为A,以腰BC为直径的半圆O切AD于点E,连接BE,若BC=6,∠EBC=30°,则梯形ABCD的面积为 .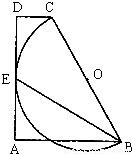
【答案】分析:连接EC,EO.根据梯形的面积等于梯形的中位线长乘以高,显然中位线即是半圆的半径,即为3.故只需求得该梯形的高.根据梯形的中位线,只需求得DE的长,首先根据30度的直角三角形BCE求得CE的长,再根据弦切角定理求得∠CED=30°,进一步根据锐角三角函数求得DE的长,再根据梯形的面积公式进行计算.
解答: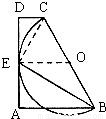 解:如图连接EC,
解:如图连接EC,
∵BC为半圆O的直径,
∴BE⊥EC(1分)
∵∠EBC=30°,
∴EC= BC=
BC= ×6=3
×6=3
连接OE,∴OE=OB=3∠BEO=30°
∵AD与⊙O相切于点E,∴OE⊥AD
∴∠OEC=60°,∴∠DEC=30°
∴DC= EC=
EC= ∴DE=
∴DE= (3分)
(3分)
∵OE∥DC∥AB,OC=OB,
∴OE是梯形的中位线∴AE=DE= (5分)
(5分)
∴AD=2DE=3
∵AD⊥AB,
∴DA为梯形ABCD的高
∴S梯形ABCD=OE•AD=3×3 .(7分)
.(7分)
故答案为:9 .
.
点评:综合运用了切线的性质定理、平行线等分线段定理、梯形的中位线定理.能够发现此图中30度的直角三角形,熟练运用特殊角的锐角三角函数值进行计算.
解答:
 解:如图连接EC,
解:如图连接EC,∵BC为半圆O的直径,
∴BE⊥EC(1分)
∵∠EBC=30°,
∴EC=
 BC=
BC= ×6=3
×6=3连接OE,∴OE=OB=3∠BEO=30°
∵AD与⊙O相切于点E,∴OE⊥AD
∴∠OEC=60°,∴∠DEC=30°
∴DC=
 EC=
EC= ∴DE=
∴DE= (3分)
(3分)∵OE∥DC∥AB,OC=OB,
∴OE是梯形的中位线∴AE=DE=
 (5分)
(5分)∴AD=2DE=3

∵AD⊥AB,
∴DA为梯形ABCD的高
∴S梯形ABCD=OE•AD=3×3
 .(7分)
.(7分)故答案为:9
 .
.点评:综合运用了切线的性质定理、平行线等分线段定理、梯形的中位线定理.能够发现此图中30度的直角三角形,熟练运用特殊角的锐角三角函数值进行计算.

练习册系列答案
相关题目
 如图,已知棱锥P-ABCD的底面ABCD为直角梯 形,AB∥CD,AB⊥BC,CD=PB=BC=1,
如图,已知棱锥P-ABCD的底面ABCD为直角梯 形,AB∥CD,AB⊥BC,CD=PB=BC=1, 如图,已知棱锥P-ABCD的底面ABCD为直角梯 形,AB∥CD,AB⊥BC,CD=PB=BC=1,
如图,已知棱锥P-ABCD的底面ABCD为直角梯 形,AB∥CD,AB⊥BC,CD=PB=BC=1,