题目内容
8．曲线$\sqrt{x}$+$\sqrt{y}$=1与两坐标轴所围成图形的面积是$\frac{1}{6}$．分析 首先由题意，画出图象，然后利用定积分表示面积
解答 解：曲线$\sqrt{x}$+$\sqrt{y}$=1，即y=（1-$\sqrt{x}$）2即图象与两坐标轴围成的图形如图阴影部分
其面积为${∫}_{0}^{1}$（1-$\sqrt{x}$）2dx=${∫}_{0}^{1}$（1-2$\sqrt{x}$+x）dx=（$\frac{1}{2}{x}^{2}-\frac{4}{3}{x}^{\frac{3}{2}}$+x）|${\;}_{0}^{1}$=$\frac{1}{6}$；
故答案为：$\frac{1}{6}$
点评 本题考查了利用定积分求曲边梯形的面积；关键是正确利用定积分表示面积，然后计算．
练习册系列答案
相关题目
18．设点P是椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）上于点，F1，F2分别是椭圆的左、右交点，I为△PF1F2的内心，若S${\;}_{△IP{F}_{1}}$+S${\;}_{△IP{F}_{2}}$=2S${\;}_{△I{F}_{1}{F}_{2}}$，则该椭圆的离心率是（ ）
| A． | $\frac{1}{4}$ | B． | $\frac{\sqrt{2}}{2}$ | C． | $\frac{1}{2}$ | D． | $\frac{\sqrt{3}}{2}$ |
19．若对?x，y∈[0，+∞），不等式4ax≤ex+y-2+ex-y-2+2恒成立，则实数a的最大值是（ ）
| A． | $\frac{1}{4}$ | B． | 1 | C． | 2 | D． | $\frac{1}{2}$ |
3．已知函数f（x）=$\left\{\begin{array}{l}{{x}^{2}+2x，x≥0}\\{{x}^{2}-2x，x＜0}\end{array}\right.$，若f（-a）+f（a）≤2f（1），则实数a的取值范围是（ ）
| A． | [-1，0） | B． | （0，1） | C． | [-1，1] | D． | [-2，2] |
20．若a＜b＜c，则下列结论中正确的是（ ）
| A． | a|c|＜b|c| | B． | ab＜bc | C． | a-c＜b-c | D． | $\frac{1}{a}＞\frac{1}{b}＞\frac{1}{c}$ |
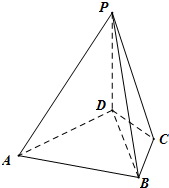如图，四棱锥P-ABCD中，PD⊥平面ABCD，△ABD是边长为3的正三角形，BC=CD=$\sqrt{3}$，PD=4．