题目内容
设函数f(x)= +bx+1(a、b为实数),F(x)=
+bx+1(a、b为实数),F(x)=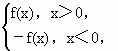
(Ⅰ)若f(-1)=0,且对任意实数均有f(x)≥0成立,求F(x)的表达式;
(Ⅱ)在(Ⅰ)的条件下,当x∈[-2,2]时,g(x)=f(x)-kx是单调函数,求实数k的取值范围;
(Ⅲ)若f(x)是偶函数,试判断F(x)的奇偶性.
(Ⅳ)设mn<0,m+n>0,且f(x)是偶函数,求证:F(m)+F(n)>0.
答案:
解析:
解析:
|
(1)∵f(-1)=0.∴b=a+1 由f(x)≥0恒成立,知△= ∴a=1,从而f(x)= ∴ (2)由(1)知,f(x)= 由g(x)在[-2,2]上是单调函数,知: ∴得k≤-2或k≥6 (3)∵f(x)为偶函数,∴f(-x)=f(x),而a>0 ∴f(x)在(0,+∞)是增函数 对于F(x),当x>0时,-x<0, F(-x)=-f(-x)=-f(x)=-F(x) x<0时,-x>0, F(-x)=f(-x)=f(x)=-F(x) ∴F(x)是奇函数,且F(x)在(0,+∞)上是增函数 由mn<0,知,m、n异号, 当m>0,n<0时,由m>-n>0知F(m)>F(-n)=-F(n) ∴F(m)+F(n)>0 当m<0,n>0时,由n>-m>0知F(n)>F(-m)=-F(m) ∴F(m)+F(n)>0 综上知:F(m)+F(n)>0, |

练习册系列答案
相关题目
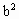 -4a=
-4a=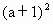 -4a=
-4a=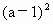 ≤0
≤0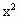 +2x+1=
+2x+1=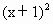
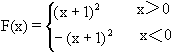
 +2x+1,∴g(x)=f(x)-kx=
+2x+1,∴g(x)=f(x)-kx=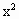 +(2-k)x+1
+(2-k)x+1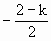 ≤-2或
≤-2或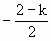 ≥2
≥2 sin2x+m).
sin2x+m). 时,-4<f(x)<4恒成立,求实数m的取值范围.
时,-4<f(x)<4恒成立,求实数m的取值范围.