题目内容
已知斜率为-2的直线与椭圆C:
+y2=1(a>0)交于A,B两点,且线段AB的中点为E(
,
).直线l2与y轴交于点M(0,m)(m≠0),与椭圆C交于相异两点P,Q,O为坐标原点,且
=λ
,
+λ
=4
,λ∈R.
(1)求椭圆C的方程;
(2)求λ的值;
(3)求m的取值范围.
| x2 |
| a2 |
| 1 |
| 2 |
| 1 |
| 2 |
| PM |
| MQ |
| OP |
| OQ |
| OM |
(1)求椭圆C的方程;
(2)求λ的值;
(3)求m的取值范围.
分析:(1)平方差法:设A(x1,y1),B(x2,y2),代入椭圆方程作差,据中点坐标公式、直线斜率公式即可求得a2值;
(2)设P(x3,y3),Q(x4,y4),l2:y=kx+m,由
,用横坐标表示出来即可求得λ值;
(3)将直线l2的方程与椭圆方程联立消y,由(2)的结论及韦达定理可得k,m的关系式,再由△>0消掉k即可求得m的取值范围;
(2)设P(x3,y3),Q(x4,y4),l2:y=kx+m,由
|
(3)将直线l2的方程与椭圆方程联立消y,由(2)的结论及韦达定理可得k,m的关系式,再由△>0消掉k即可求得m的取值范围;
解答:解:(1)设A(x1,y1),B(x2,y2),则x1+x2=1,y1+y2=1,
=-2.
∵
+y12=1,
+y22=1,
∴两式相减得
+(y1+y2)(y1-y2)=0,即
+(y1+y2)
=0,即
+1×(-2)=0,得a2=
,
所以椭圆C的方程为2x2+y2=1.
(2)设P(x3,y3),Q(x4,y4),l2:y=kx+m(∵l2与y轴相交,∴l2的斜率存在).
由
,得
,得
,
即
,将①代入②得(λ-3)m=0,
∵m≠0,∴λ=3.
(3)将y=kx+m代入2x2+y2=1,得(k2+2)x2+2kmx+(m2-1)=0.
∵λ=3,
∴由
消去x3、x4得,k2=
.
由△>0得k2>2(m2-1),即
>2(m2-1),即
<0,即
<0,解得-1<m<-
,或
<m<1.
所以m的取值范围为-1<m<-
,或
<m<1.
| y1-y2 |
| x1-x2 |
∵
| x12 |
| a2 |
| x22 |
| a2 |
∴两式相减得
| (x1+x2)(x1-x2) |
| a2 |
| x1+x2 |
| a2 |
| y1-y2 |
| x1-x2 |
| 1 |
| a2 |
| 1 |
| 2 |
所以椭圆C的方程为2x2+y2=1.
(2)设P(x3,y3),Q(x4,y4),l2:y=kx+m(∵l2与y轴相交,∴l2的斜率存在).
由
|
|
|
即
|
∵m≠0,∴λ=3.
(3)将y=kx+m代入2x2+y2=1,得(k2+2)x2+2kmx+(m2-1)=0.
∵λ=3,
∴由
|
| 2(1-m2) |
| 4m2-1 |
由△>0得k2>2(m2-1),即
| 2(1-m2) |
| 4m2-1 |
| (m2-1)m2 |
| 4m2-1 |
| (m+1)(m-1) |
| (2m+1)(2m-1) |
| 1 |
| 2 |
| 1 |
| 2 |
所以m的取值范围为-1<m<-
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查直线与圆锥曲线的综合问题,考查学生综合运用所学知识分析问题解决问题的能力,弦长公式、韦达定理、判别式是解决该类问题的基础知识,应熟练掌握,涉及弦中点问题常考虑“平方差法”.

练习册系列答案
相关题目
已知斜率为2的直线l过抛物线y2=ax的焦点F,且与y轴相交于点A,若△OAF(O为坐标原点)的面积为4,则抛物线方程为( )
| A、y2=4x | B、y2=8x | C、y2=4x或y2=-4x | D、y2=8x或y2=-8x |
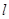 双曲线
双曲线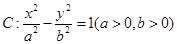 交
交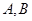 两点,若点
两点,若点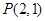 是
是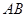 的中点,则
的中点,则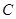 的离心率等于( )
的离心率等于( )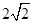 (B)
2 (C)
(B)
2 (C) 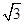 (D)
(D)