题目内容
已知椭圆![]() ,其相应于焦点F(2,0)的准线方程为x=4.
,其相应于焦点F(2,0)的准线方程为x=4.
(Ⅰ)求椭圆C的方程;
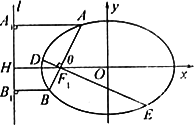
(Ⅱ)已知过点F1(-2,0)倾斜角为![]() 的直线交椭圆C于A,B两点,求证:
的直线交椭圆C于A,B两点,求证:![]() ;
;
(Ⅲ)过点F1(-2,0)作两条互相垂直的直线分别交椭圆C于A,B和D,E,求|AB|+|DE|的最小值.
答案:
解析:
解析:
|
解:本题主要考查直线的方程、椭圆的方程和性质、直线与线段椭圆的位置关系等知识,考查数形结合的数学思想运算能力和综合解题能力.本小题满分14分. (Ⅰ)由题意得: (Ⅱ)方法一: 由(Ⅰ)知 设 作
方法二: 当 将其代入方程 设 当 (Ⅲ)设直线 当 |

练习册系列答案
相关题目
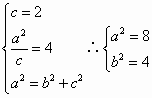
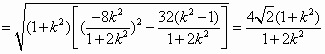 (1)
(1)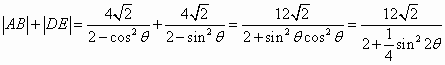 .
.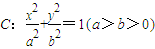 ,其相应于焦点F(2,0)的准线方程为x=4.
,其相应于焦点F(2,0)的准线方程为x=4.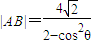 ;
;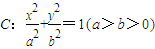 ,其相应于焦点F(2,0)的准线方程为x=4.
,其相应于焦点F(2,0)的准线方程为x=4.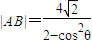 ;
;