题目内容
已知椭圆![]() ,其相应于焦点F(2,0)的准线方程为x=4.
,其相应于焦点F(2,0)的准线方程为x=4.
(Ⅰ)求椭圆C的方程;
(Ⅱ)已知过点F1(-2,0)倾斜角为![]() 的直线交椭圆C于A,B两点.
的直线交椭圆C于A,B两点.
求证:![]()
(Ⅲ)过点F1(-2,0)作两条互相垂直的直线分别交椭圆C于点A、B和D、E,求![]() 的最小值.
的最小值.
解:(Ⅰ)由题意得:
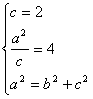 ,
,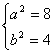
∴椭圆C的方程为![]() 。
。
(Ⅱ)方法一:
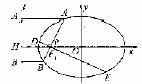
由(Ⅰ)知,![]() 是椭圆C的左焦点,离心率
是椭圆C的左焦点,离心率![]()
设![]() 为椭圆的左准线,则
为椭圆的左准线,则![]()
![]() ,
,
作![]() 于
于![]() ,
,![]() 于
于![]() ,
,![]() 与
与![]() 轴交于点H(如图)
轴交于点H(如图)
∵点A在椭圆上,
∴![]()
![]()
∴![]()
同理![]()
∴![]() 。
。
方法二:
当![]() 时,记
时,记![]() ,则AB
,则AB![]() ,
,
将其代入方程![]()
得![]()
设![]() ,则
,则![]() 是此二次方程的两个根。
是此二次方程的两个根。
∴![]() ,
,
![]()
![]()
![]() ①
①
∵![]() ,代入①式得
,代入①式得![]() ②
②
当![]() 时,
时,![]() 仍满足②式
仍满足②式
∴![]()
(Ⅲ)设直线AB的倾斜角为![]() ,由于
,由于![]() ,由(Ⅱ)可得,
,由(Ⅱ)可得,
![]() ,
,![]()
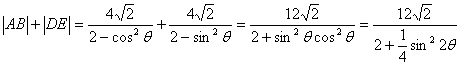
当![]() 或
或![]() ,
,![]() 取得最小值
取得最小值![]() 。
。

练习册系列答案
相关题目
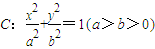 ,其相应于焦点F(2,0)的准线方程为x=4.
,其相应于焦点F(2,0)的准线方程为x=4.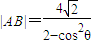 ;
;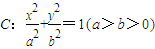 ,其相应于焦点F(2,0)的准线方程为x=4.
,其相应于焦点F(2,0)的准线方程为x=4.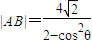 ;
;