题目内容
我们规定:对于任意实数A,若存在数列{an}和实数x(x≠0),使得A=a1+a2x+a3x2+…anxn-1,则称数A可以表示成x进制形式,简记为A=
.如:A=
,则表示A是一个2进制形式的数,且A=-1+3×2+(-2)×22+1×23=5.
(I)已知m=(1-2x)(1+3x2)(其中x≠0),试将m表示成x进制的简记形式;
(II)记bn=
(n∈N*),若{an}是等差数列,且满足a1+a2=3,a3+a4=7,求bn=9217时n的值.
. |
| x~(a1)(a2)(a3)…(an-1)(an) |
. |
| 2~(-1)(3)(-2)(1) |
(I)已知m=(1-2x)(1+3x2)(其中x≠0),试将m表示成x进制的简记形式;
(II)记bn=
. |
| 2~(a1)(a2)(a3)…(an-1)(an) |
分析:(Ⅰ)由m=(1-2x)(1+3x2)=1-2x+3x2-6x3,能将m表示成x进制的简记形式.
(Ⅱ)由{an}是等差数列,即已知条件利用通项公式即可得出an,利用“错位相减法”即可得出bn,进而解出n.
(Ⅱ)由{an}是等差数列,即已知条件利用通项公式即可得出an,利用“错位相减法”即可得出bn,进而解出n.
解答:解:(I)由m=(1-2x)(1+3x2)=1-2x+3x2-6x3=
.
(Ⅱ)∵{an}是等差数列,设公差为d,又a1+a2=3,a3+a4=7,
∴
,解得
,
∴an=1+(n-1)×1=n.
bn=1+2×21+3×22+…+n×2n-1,
2bn=1×2+2×22+3×23+…+(n-1)×2n-1+n×2n,
两式相减得-bn=1+2+22+…+2n-1-n×2n
∴-bn=
-n×2n,
∴bn=(n-1)×2n+1.
又bn=9217,∴(n-1)×2n+1=9217,解得n=10.
. |
| x~(1)(-2)(3)(-6) |
(Ⅱ)∵{an}是等差数列,设公差为d,又a1+a2=3,a3+a4=7,
∴
|
|
∴an=1+(n-1)×1=n.
bn=1+2×21+3×22+…+n×2n-1,
2bn=1×2+2×22+3×23+…+(n-1)×2n-1+n×2n,
两式相减得-bn=1+2+22+…+2n-1-n×2n
∴-bn=
| 2n-1 |
| 2-1 |
∴bn=(n-1)×2n+1.
又bn=9217,∴(n-1)×2n+1=9217,解得n=10.
点评:本题考查数列的递推公式即新定义,解题时要认真审题,仔细解答,注意挖掘题设的隐含条件,合理地进行等价转化.数列掌握等差数列和等比数列的通项公式和前n项和公式及其“错位相减法”是解题的关键.

练习册系列答案
 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案
相关题目
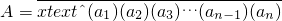 .如:
.如: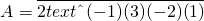 ,则表示A是一个2进制形式的数,且A=-1+3×2+(-2)×22+1×23=5.
,则表示A是一个2进制形式的数,且A=-1+3×2+(-2)×22+1×23=5.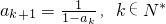 ,
,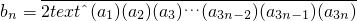 (n∈N*),是否存在实常数p和q,对于任意的n∈N*,bn=p•8n+q总成立?若存在,求出p和q;若不存在,说明理由.
(n∈N*),是否存在实常数p和q,对于任意的n∈N*,bn=p•8n+q总成立?若存在,求出p和q;若不存在,说明理由.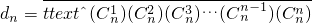 ,求
,求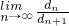 .
. .如:
.如: ,则表示A是一个2进制形式的数,且A=-1+3×2+(-2)×22+1×23=5.
,则表示A是一个2进制形式的数,且A=-1+3×2+(-2)×22+1×23=5. ,
, (n∈N*),是否存在实常数p和q,对于任意的n∈N*,bn=p•8n+q总成立?若存在,求出p和q;若不存在,说明理由.
(n∈N*),是否存在实常数p和q,对于任意的n∈N*,bn=p•8n+q总成立?若存在,求出p和q;若不存在,说明理由. ,求
,求 .
.