题目内容
为了考察冰川的融化状况,一支科考队在某冰川山上相距8Km的A、B两点各建一个考察基地,视冰川面为平面形,以过A、B两点的直线为x轴,线段AB的垂直平分线为y轴建立平面直角坐标系(如图).考察范围到A、B两点的距离之和不超过10Km的区域.(1)求考察区域边界曲线的方程:
(2)如图所示,设线段P1P2(3)是冰川的部分边界线(不考虑其他边界),当冰川融化时,边界线沿与其垂直的方向朝考察区域平行移动,第一年移动0.2km,以后每年移动的距离为前一年的2倍.问:经过多长时间,点A恰好在冰川边界线上?

【答案】分析:(1)设边界曲线上点P的坐标为(x,y),由|PA|+|PB|=10知,点P在以A、B为焦点、长轴长为2a=10的椭圆上.由此可知考察区域边界曲线的方程为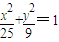 .
.
(2)由题意知过点P1,P2的直线方程为4x-3y+47=0.因此点A到直线P1P2的距离为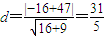 ,设经过n年,点A恰好在冰川边界上,则利用等比数列求和公式可得
,设经过n年,点A恰好在冰川边界上,则利用等比数列求和公式可得 ,由此可知经过5年,点A恰好在冰川边界上.
,由此可知经过5年,点A恰好在冰川边界上.
解答:解:(1)设边界曲线上点P的坐标为(x,y),
由|PA|+|PB|=10知,点P在以A、B为焦点、长轴长为2a=10的椭圆上.
此时 ,
,
∴考察区域边界曲线的方程为 .
.
(2)由题意知过点P1,P2的直线方程为4x-3y+47=0.
因此点A到直线P1P2的距离为 ,
,
设经过n年,点A恰好在冰川边界上,
则利用等比数列求和公式可得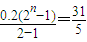 ,
,
解得n=5,
即经过5年,点A恰好在冰川边界上.
点评:本题考查椭圆的性质和等比数列的知识,解题时要注意公式的灵活运用.
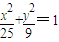 .
.(2)由题意知过点P1,P2的直线方程为4x-3y+47=0.因此点A到直线P1P2的距离为
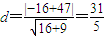 ,设经过n年,点A恰好在冰川边界上,则利用等比数列求和公式可得
,设经过n年,点A恰好在冰川边界上,则利用等比数列求和公式可得 ,由此可知经过5年,点A恰好在冰川边界上.
,由此可知经过5年,点A恰好在冰川边界上.解答:解:(1)设边界曲线上点P的坐标为(x,y),
由|PA|+|PB|=10知,点P在以A、B为焦点、长轴长为2a=10的椭圆上.
此时
 ,
,∴考察区域边界曲线的方程为
 .
.(2)由题意知过点P1,P2的直线方程为4x-3y+47=0.
因此点A到直线P1P2的距离为
 ,
,设经过n年,点A恰好在冰川边界上,
则利用等比数列求和公式可得
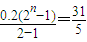 ,
,解得n=5,
即经过5年,点A恰好在冰川边界上.
点评:本题考查椭圆的性质和等比数列的知识,解题时要注意公式的灵活运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
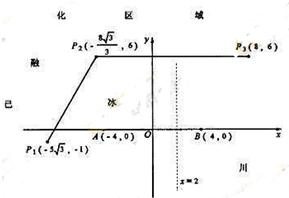
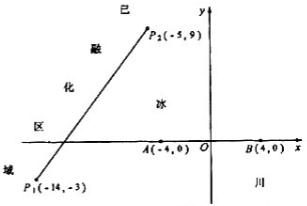 为了考察冰川的融化状况,一支科考队在某冰川山上相距8Km的A、B两点各建一个考察基地,视冰川面为平面形,以过A、B两点的直线为x轴,线段AB的垂直平分线为y轴建立平面直角坐标系(如图).考察范围到A、B两点的距离之和不超过10Km的区域.
为了考察冰川的融化状况,一支科考队在某冰川山上相距8Km的A、B两点各建一个考察基地,视冰川面为平面形,以过A、B两点的直线为x轴,线段AB的垂直平分线为y轴建立平面直角坐标系(如图).考察范围到A、B两点的距离之和不超过10Km的区域. km的区域;在直线x=2的左侧,考察范围为到A,B两点的距离之和不超过4
km的区域;在直线x=2的左侧,考察范围为到A,B两点的距离之和不超过4 km的区域,
km的区域, 
