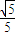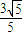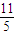Question

已知点A的坐标是（1-t，1-t，t），点B的坐标是（2，t，t），则A与B两点间距离的最小值为（　　）

• A．

  5

  5

• B．

  55

  5

• C．

  3 5

  5

• D．

  11

  5

Answer 1

分析：利用两点间的距离公式，结合配方法，即可求最值．

解答：解：∵点A的坐标是（1-t，1-t，t），点B的坐标是（2，t，t），
∴AB=

(t+1)2+(2t-1)2

=

5t2-2t+2

=

5(t- 1 5 )2+ 9 5

∴t=

1

5

时，A与B两点间距离的最小值为

3 5

5

故选C．

点评：本题考查两点间的距离公式，考查配方法的运用，考查学生的计算能力，属于基础题．