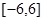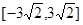题目内容
若两个非零向量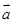 ,
,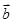 满足
满足 ,则向量
,则向量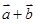 与
与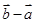 的夹角为( )
的夹角为( )
A. | B.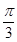 | C.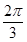 | D.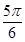 |
B
解析试题分析:根据题意,由于两个非零向量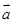 ,
,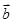 满足
满足 ,说明两个向量
,说明两个向量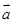 ,
,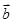 垂直,同时平方后可知,
垂直,同时平方后可知, 向量
向量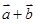 与
与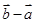 即为
即为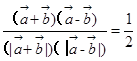 ,故可知夹角为
,故可知夹角为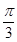 ,选B.
,选B.
考点:向量的数量积运用
点评:解决的关键是利用向量的数量积性质来表示向量的夹角,属于基础题。

练习册系列答案
相关题目
若向量 满足
满足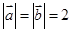 ,且
,且 ,则向量
,则向量 的夹角为
的夹角为
| A.30° | B.45° | C.60° | D.120° |
在平行四边形ABCD中,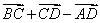 等于( )
等于( )
A. | B.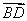 | C.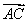 | D. |
已知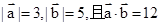 ,则向量
,则向量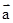 在向量
在向量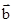 上的投影为( )
上的投影为( )
A.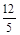 | B.3 | C.4 | D.5 |
设 为基底向量,已知向量
为基底向量,已知向量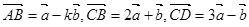 ,若
,若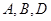 三点共线,则实数
三点共线,则实数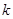 的值等于
的值等于
A.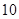 | B.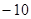 | C.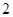 | D. |
已知向量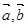 ,满足
,满足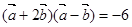 ,且
,且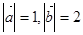 ,则
,则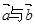 的夹角为( )
的夹角为( )
A.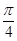 | B.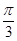 | C.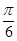 | D. |
椭圆M: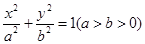 长轴上的两个顶点为
长轴上的两个顶点为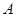 、
、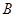 ,点P为椭圆M上除
,点P为椭圆M上除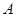 、
、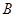 外的一个动点,若
外的一个动点,若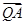 ·
· =0,
=0,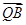 ·
·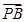 =0,则动点Q在下列哪种曲线上( )
=0,则动点Q在下列哪种曲线上( )
| A.圆 | B.椭圆 | C.双曲线 | D.抛物线 |
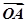 =
=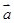 ,
,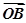 =
=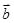 ,其中
,其中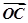 =λ
=λ
 :
: ,四边形
,四边形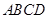 为圆
为圆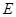 、
、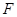 分别为边
分别为边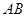 、
、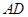 的中点,当正方形
的中点,当正方形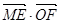 的取值范围是( )
的取值范围是( )