题目内容
椭圆M: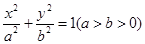 长轴上的两个顶点为
长轴上的两个顶点为 、
、 ,点P为椭圆M上除
,点P为椭圆M上除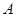 、
、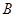 外的一个动点,若
外的一个动点,若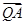 ·
· =0,
=0,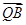 ·
·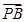 =0,则动点Q在下列哪种曲线上( )
=0,则动点Q在下列哪种曲线上( )
| A.圆 | B.椭圆 | C.双曲线 | D.抛物线 |
B
解析试题分析:A坐标为(-a,0),B坐标为(a,0)
设Q坐标为(m,n),P坐标为(s,t)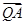 ·
· =(-a-m)(-a-s)+(-n)(-t)=0
=(-a-m)(-a-s)+(-n)(-t)=0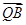 ·
·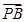 =(a-m)(a-s)+(-n)(-t)=0
=(a-m)(a-s)+(-n)(-t)=0
解得:s=-m,t=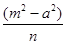
又P在M上,∴s=asint,t=bcost
解得:m=-asint,n=- cost/b
cost/b
即: +
+ =1
=1
所以点Q(m,n)应该是在一个椭圆上
考点:本试题考查了向量的数量积的运用。
点评:本试题利用数量积为姆拜哦,结合坐标法来表示向量,然后得到坐标的关系式,进而确定出点Q的坐标满足的关系式,属于中档题。

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案
相关题目
若两个非零向量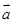 ,
,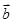 满足
满足 ,则向量
,则向量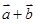 与
与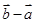 的夹角为( )
的夹角为( )
A. | B.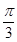 | C.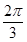 | D.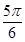 |
已知向量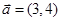 ,
, 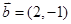 ,如果向量
,如果向量 与
与 垂直,则
垂直,则 的值为( )
的值为( )
A.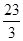 | B.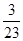 | C.2 | D.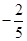 |
已知 ,则
,则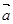 在
在 方向上的投影为( )
方向上的投影为( )
A.-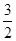 | B.- | C.-2 | D.-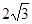 |
已知平面向量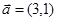 ,
,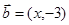 ,且
,且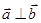 ,则
,则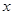 的值为( )
的值为( )
| A.-3 | B.-1 | C.1 | D.3 |
O是锐角三角形ABC的外心,由O向边BC,CA,AB引垂线,垂足分别是D,E,F,给出下列命题:
① ;
;
②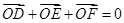 ;
;
③ :
: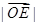 :
: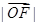 =cosA:cosB:cosC;
=cosA:cosB:cosC;
④ ,使得
,使得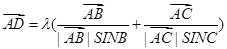 。
。
以上命题正确的个数是( )
| A.1 | B.2 | C.3 | D.4; |
已知平行四边形 的三个顶点的坐标分别为
的三个顶点的坐标分别为 ,
, ,
, ,则顶点
,则顶点 的坐标为( )
的坐标为( )
| A.(2,2) | B.(-2,2) | C.(2,-2) | D.(-2,-2) |
 、
、 、
、 ,且满足
,且满足 ,|
,|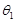 ,
,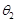 ,
, ,则它们的大小关系是( )
,则它们的大小关系是( )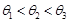


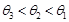
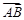 |=a,|
|=a,|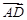 |=b,则
|=b,则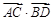 =
=