题目内容
设函数
(1)若f(x)在x=0处的极限存在,求a,b的值;
(2)若f(x)在x=0处连续,求a,b的值.
【答案】分析:(1)若f(x)在x=0处的极限存在则 -1=
-1=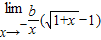 ,从而可求a,b
,从而可求a,b
(2))若f(x)在x=0处连续则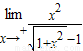 -1=
-1=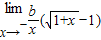 =f(0),从而可求a,b
=f(0),从而可求a,b
解答:解:(1)若f(x)在x=0处的极限存在
则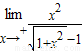 -1=
-1=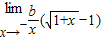
∴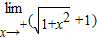 -1=
-1=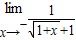 •b
•b
∴1=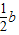
∴a∈R,b=2
(2))若f(x)在x=0处连续
则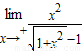 -1=
-1=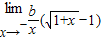 =f(0)
=f(0)
同(1)可得,b=2,且f(0)=a=1
∴a=1,b=2
点评:本题主要考查了函数的极限存在的条件与函数连续的条件的应用,解题的关键是熟练求解该题中极限,但要注意极限存在与函数连续的区别
 -1=
-1=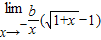 ,从而可求a,b
,从而可求a,b(2))若f(x)在x=0处连续则
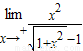 -1=
-1=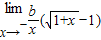 =f(0),从而可求a,b
=f(0),从而可求a,b解答:解:(1)若f(x)在x=0处的极限存在
则
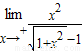 -1=
-1=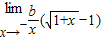
∴
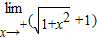 -1=
-1=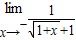 •b
•b∴1=
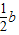
∴a∈R,b=2
(2))若f(x)在x=0处连续
则
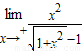 -1=
-1=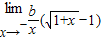 =f(0)
=f(0)同(1)可得,b=2,且f(0)=a=1
∴a=1,b=2
点评:本题主要考查了函数的极限存在的条件与函数连续的条件的应用,解题的关键是熟练求解该题中极限,但要注意极限存在与函数连续的区别

练习册系列答案
相关题目

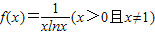
 对任意x∈(0,1)成立,求实数a的取值范围.
对任意x∈(0,1)成立,求实数a的取值范围.