题目内容
(2012•湛江二模)设x=1是函数f(x)=
e-ax的一个极值点(a>0,e为自然对数的底).
(1)求a与b的关系式(用a表示b),并求f(x)的单调区间;
(2)设m>-1,若f(x)在闭区间[m,m+1]上的最小值为0,最大值为
e-a,求m与a的值.
| x+b |
| x+1 |
(1)求a与b的关系式(用a表示b),并求f(x)的单调区间;
(2)设m>-1,若f(x)在闭区间[m,m+1]上的最小值为0,最大值为
| 1 |
| 2 |
分析:(1)因为x=1是函数f(x)=
e-ax的一个极值点,所以f′(1)=0,先将x=1代入f′(x),即可得a与b的关系式,再将f′(x)中的b用a代换,通过解不等式即可求得函数的单调区间.
(2)当-1<m≤0时,由(1)知f(x)在闭区间[m,m+1]上是增函数,所以f(m)=0,且f(m+1)=
e-a,解方程无解;当m≥1时,由(1)知f(x)在闭区间[m,m+1]上是减函数,所以f(m+1)=0,解方程无解;当0<m<1时,由(1)知f(x)在区间[m,1]上是增函数,在区间[1,m+1]上是减函数,所以f(1)=
e-a,f(m)=0,解方程即可获解
| x+b |
| x+1 |
(2)当-1<m≤0时,由(1)知f(x)在闭区间[m,m+1]上是增函数,所以f(m)=0,且f(m+1)=
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:(1)f′(x)=-
e-ax
由已知有:f′(1)=0,
∴a+(ab+a)+ab+b-1=0,
∴b=
(3分)
从而f′(x)=-
e-ax
令f′(x)=0得:x1=1,x2=-
.
∵a>0∴x2<-1
当x变化时,f′(x)、f(x)的变化情况如下表:
从上表可知:f(x)在(-∞,-
),(1,+∞)上是减函数;
在(-
,-1),(-1,1)上是增函数
(2)∵m>-1,由( I)知:
①当-1<m≤0时,m+1≤1,f(x)在闭区间[m,m+1]上是增函数.
∴f(m)=0,且f(m+1)=
e-a.
化简得:b=-m,
=eam.
又
>1,eam<1.故此时的a,m不存在
②当m≥1时,f(x)在闭区间[m,m+1]上是减函数.
又x>1时f(x)=
e-ax=
e-ax>0.其最小值不可能为0
∴此时的a,m也不存在
③当0<m<1时,m+1∈(1,2)
则最大值为f(1)=
e-a,得:b=0,a=
又f(m+1)>0,f(x)的最小值为f(m)=0,
∴m=-b=0.
综上知:m=0.a=
| [ax2+(ab+a)x+ab+b-1] |
| (x+1)2 |
由已知有:f′(1)=0,
∴a+(ab+a)+ab+b-1=0,
∴b=
| 1-2a |
| 2a+1 |
从而f′(x)=-
a(x-1)(x+
| ||
| (x+1)2 |
令f′(x)=0得:x1=1,x2=-
| 2a+3 |
| 2a+1 |
∵a>0∴x2<-1
当x变化时,f′(x)、f(x)的变化情况如下表:
| x | (-∞,x2) | (x2,-1) | (-1,1) | (1,+∞) |
| f′(x) | - | + | + | - |
| f(x) | 减函数 | 增函数 | 增函数 | 减函数 |
| 2a+3 |
| 2a+1 |
在(-
| 2a+3 |
| 2a+1 |
(2)∵m>-1,由( I)知:
①当-1<m≤0时,m+1≤1,f(x)在闭区间[m,m+1]上是增函数.
∴f(m)=0,且f(m+1)=
| 1 |
| 2 |
化简得:b=-m,
| 2 |
| m+2 |
又
| 2 |
| m+2 |
②当m≥1时,f(x)在闭区间[m,m+1]上是减函数.
又x>1时f(x)=
| x+b |
| x+1 |
x-1+
| ||
| x+1 |
∴此时的a,m也不存在
③当0<m<1时,m+1∈(1,2)
则最大值为f(1)=
| 1 |
| 2 |
| 1 |
| 2 |
又f(m+1)>0,f(x)的最小值为f(m)=0,
∴m=-b=0.
综上知:m=0.a=
| 1 |
| 2 |
点评:本题综合考查了导数在函数单调性、极值、最值问题中的应用,考查了分类讨论的思想,运算量和思维量都较大,解题时要细致运算,耐心讨论

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 (2012•湛江二模)某市为了解今年高中毕业生的身体素质状况,从本市某校高中毕业班中抽取一个班进行实心球测试,成绩在8米及以上的为合格.把所得数据进行整理后,分成6组画出频率分布直方图的一部分(如图),已知第一小组为[5,6),从左到右前5个小组的频率分别为0.06,0.10,0.14,0.28,0.30.第6小组的频数是6.
(2012•湛江二模)某市为了解今年高中毕业生的身体素质状况,从本市某校高中毕业班中抽取一个班进行实心球测试,成绩在8米及以上的为合格.把所得数据进行整理后,分成6组画出频率分布直方图的一部分(如图),已知第一小组为[5,6),从左到右前5个小组的频率分别为0.06,0.10,0.14,0.28,0.30.第6小组的频数是6.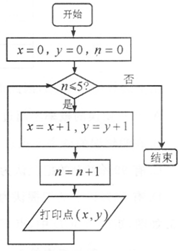 (2012•湛江二模)运行如图所示框图,坐标满足不等式组
(2012•湛江二模)运行如图所示框图,坐标满足不等式组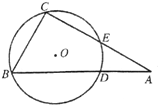 (2012•湛江二模)如图,Rt△ABC中,∠C=90°,∠A=30°,圆O经过B、C且与AB、AC分别相交于D、E.若AE=EC=
(2012•湛江二模)如图,Rt△ABC中,∠C=90°,∠A=30°,圆O经过B、C且与AB、AC分别相交于D、E.若AE=EC=