题目内容
已知如下等式:12=| 1×2×3 |
| 6 |
| 2×3×5 |
| 6 |
| 3×4×7 |
| 6 |
分析:解答此类的方法是从特殊的前几个式子进行分析找出规律.观察前几个式子的变化规律,从中猜想12+22+32+…+n2的值.再用数学归纳法证明,证明时分为两个步骤,第一步,先证明当当n=1时,命题成立,第二步,先假设当n=k时,原式成立,利用此假设证明当n=k+1时,结论也成立即可.
解答:解:由已知,猜想12+22+32+…+n2=
,
下面用数学归纳法给予证明:
(1)当n=1时,由已知得原式成立;
(2)假设当n=k时,原式成立,即12+22+32+…+k2=
,
那么,当n=k+1时,12+22+32+…+(k+1)2=
+(k+1)2
=
=
故n=k+1时,原式也成立.
由(1)、(2)知12+22+32+…+n2=
成立.
| n(n+1)(2n+1) |
| 6 |
下面用数学归纳法给予证明:
(1)当n=1时,由已知得原式成立;
(2)假设当n=k时,原式成立,即12+22+32+…+k2=
| k(k+1)(2k+1) |
| 6 |
那么,当n=k+1时,12+22+32+…+(k+1)2=
| k(k+1)(2k+1) |
| 6 |
=
| (k+1)(k+2)(2k+3) |
| 6 |
=
| (k+1)[(k+1)+1][2(k+1)+1] |
| 6 |
故n=k+1时,原式也成立.
由(1)、(2)知12+22+32+…+n2=
| n(n+1)(2n+1) |
| 6 |
点评:本题主要考查归纳推理、数学归纳法,数学归纳法的基本形式:设P(n)是关于自然数n的命题,若1°P(n0)成立(奠基);2°假设P(k)成立(k≥n0),可以推出P(k+1)成立(归纳),则P(n)对一切大于等于n0的自然数n都成立.

练习册系列答案
相关题目
 ,
,  ,
, ,当
,当 时,试猜想
时,试猜想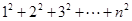 的值,并用数学归纳法给予证明。
的值,并用数学归纳法给予证明。