题目内容
已知如下等式:12=
,12+22=
,12+22+32=
,…当n∈N*时,试猜想12+22+32+…+n2的值,并用数学归纳法给予证明.
| 1×2×3 |
| 6 |
| 2×3×5 |
| 6 |
| 3×4×7 |
| 6 |
由已知,猜想12+22+32+…+n2=
,
下面用数学归纳法给予证明:
(1)当n=1时,由已知得原式成立;
(2)假设当n=k时,原式成立,即12+22+32+…+k2=
,
那么,当n=k+1时,12+22+32+…+(k+1)2=
+(k+1)2
=
=
故n=k+1时,原式也成立.
由(1)、(2)知12+22+32+…+n2=
成立.
| n(n+1)(2n+1) |
| 6 |
下面用数学归纳法给予证明:
(1)当n=1时,由已知得原式成立;
(2)假设当n=k时,原式成立,即12+22+32+…+k2=
| k(k+1)(2k+1) |
| 6 |
那么,当n=k+1时,12+22+32+…+(k+1)2=
| k(k+1)(2k+1) |
| 6 |
=
| (k+1)(k+2)(2k+3) |
| 6 |
=
| (k+1)[(k+1)+1][2(k+1)+1] |
| 6 |
故n=k+1时,原式也成立.
由(1)、(2)知12+22+32+…+n2=
| n(n+1)(2n+1) |
| 6 |

练习册系列答案
相关题目
 ,
,  ,
, ,当
,当 时,试猜想
时,试猜想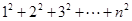 的值,并用数学归纳法给予证明。
的值,并用数学归纳法给予证明。