题目内容
(本题13分)
向量 =(
=( +1,
+1, ),
), =(1,4cos(x
=(1,4cos(x +)),设函数
+)),设函数 =
= (
( ∈R,且
∈R,且 为常数).
为常数).
(1)若 为任意实数,求
为任意实数,求 的最小正周期;
的最小正周期;
(2)若 在[0,)上的最大值与最小值之和为7,求
在[0,)上的最大值与最小值之和为7,求 的值.
的值.
解: g(x)=mn=a+1+4sinxcos(x+)
=sin2x-2sin2x+a+1
=sin2x+cos2x+a
=2sin(2x+)+a
(1)g(x)=2sin(2x+)+a,T=π.
(2)∵0≤x<,∴≤2x+<
当2x+=,即 x=时,ymax=2
x=时,ymax=2 +a.
+a.
当2x+=,即x=0时,ymin=1+a,
故a+1+2+a=7,即a=2.
解析

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
设  为单位向量,若
为单位向量,若 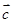 满足
满足 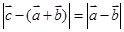 ,则
,则  的最大值为
的最大值为
A. | B.2 | C. | D.1 |
如图, 是
是 所在的平面内一点,且满足
所在的平面内一点,且满足 ,
, 是
是 的三等分点,则( )
的三等分点,则( )
A. | B. |
C. | D. |
已知 为
为 所在平面上一点,若
所在平面上一点,若 ,则
,则 为
为 的( )
的( )
| A.内心 | B.外心 | C.垂心 | D.重心 |
 为非零向量,且
为非零向量,且

 ,求
,求 与
与 的夹角
的夹角 。
。 与
与 ,其中
,其中 。
。 若
若 ,求
,求 和
和 的值;
的值; 若
若 ,求
,求 的值域。
的值域。 ,令
,令
 的周期为
的周期为 .
. 的解析式;
的解析式; 时
时 ,求实数
,求实数 的取值范围.
的取值范围.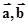 满足
满足 及
及
 的值.
的值. 与
与 的夹角为
的夹角为 ,定义
,定义 为
为 ,若
,若 ,
, ,则
,则 ( )
( ) B.
B.



