题目内容
已知{an}是等差数列,a1=-9,S3=S7,那么使其前n项和Sn最小的n是( )
| A、4 | B、5 | C、6 | D、7 |
分析:先由等差数列的前n项和公式Sn=
n2+(a1-
)n知道其可以表示为过原点的抛物线,再利用a1=-9=s1<0,S3=S7,画出其对应图象,由图象即可得出结论.
| d |
| 2 |
| d |
| 2 |
解答: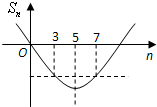 解:因为等差数列的前n项和Sn=
解:因为等差数列的前n项和Sn=
n2+(a1-
)n可表示为过原点的抛物线,
又本题中a1=-9=s1<0,S3=S7,可表示如图,
由图可知,n=
=5是抛物线的对称轴,
所以n=5时Sn最小,
故选 B
 解:因为等差数列的前n项和Sn=
解:因为等差数列的前n项和Sn=| d |
| 2 |
| d |
| 2 |
又本题中a1=-9=s1<0,S3=S7,可表示如图,
由图可知,n=
| 3+7 |
| 2 |
所以n=5时Sn最小,
故选 B
点评:本题主要考查等差数列的前n项和公式以及数形结合思想的应用,考查分析问题和解决问题的能力,属于基础题目.

练习册系列答案
相关题目
 满足:
满足: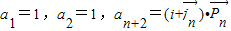 .
.